Numerical Aperture and Resolution

The magnification of a convex lens is the ratio of the distance from the object to the lens and the lens to the image. As the object approaches the focal point of the lens, the ratio increases without limit. If the focal length of the microscoope objective lens is sufficiently short, it seems possible to magnify not by a factor of 1000, but by a factor of 10,000 or more.

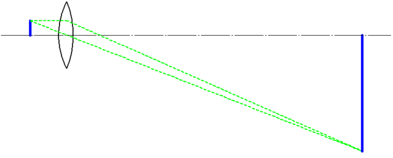
Fig. 1.  Enlargement of a geometrical optical image. The magnification can be increased without limitation.

where α is a constant of the order of 1. The NA is defined as

NA = n sin θ (2)

using the angle θ formed by the optical axis in a focused state and the light beam passing through the outermost periphery of the objective lens. Here, n is the refractive index of a medium between the front surface of the objective lens and the sample. In the case of a dry objective lens, it is the refractive index of air (=1), and in the case of an oil immersion objective lens, it is the refractive index of an oil immersion liquid (about 1.5). Since the maximum value of sin θ is 1, the maximum value of NA of the dry objective lens is 1. In general, the higher the magnification of the objective lens, the larger the NA. When comparing the achromat and the apochromat, the NA of the apochromat is larger at the same magnification.

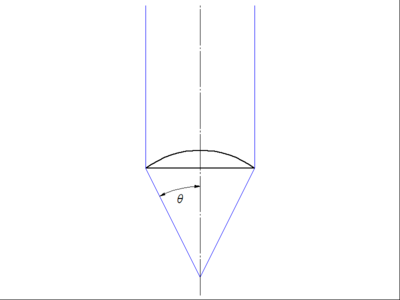
Fig. 2 The sine of the angle θ formed by the light beam passing through the optical axis and the outermost periphery of the lens when in focus is the numerical aperture.

Since NA is less than 1 for a dry objective lens and less than 1.5 for an oil immersion objective lens, Eq. (1) shows that the limit of the smallest structure that can be observed with an optical microscope is the order of the wavelength of the light used for observation.

NA and microscopy resolution

Here, we will explain the physics behind Eq. (1) based on the derivation by Abbe. The physical background of Equation (1) is shown using the observation image of a cross grating. The cross grating of 196 lines/mm was used. The first order diffraction angle of the grating for 550 nm light is 6.2 degrees, and corresponding NA is about 0.11.

dsinθ=mλ　…………(3)

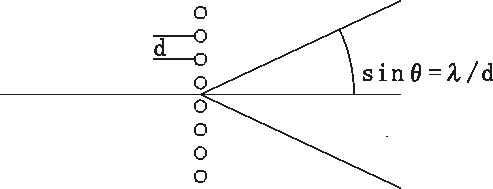
Abbe found that to observe a diffraction grating image under a microscope, at least the first order diffracted light must be captured by the objective lens together with the zeroth order light. In other words, a diffraction grating image can be observed only with an objective lens whose NA is greater than the sine of the first order diffraction angle of  the grating.

Below is the cross diffraction grating image and the diffraction pattern image at that time. If you want to know how the diffraction pattern was photographed, please see the "Objective lens back focal plane and Bertrand lens" part near the end of this text.

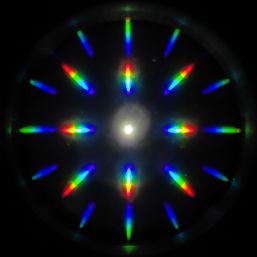
Fig. 3 Cross diffraction grating and its diffraction pattern

The white spot at the center of the diffraction pattern on the right is the 0th-order light that went straight without diffraction. As can be seen from the figure, the 1st order diffraction includes the entire visible spectrum from blue to red, but the red part of the diffracted light is not captured at the outer periphery. We can continue the discussion as it is, but we decided to use a monochromatic filter to make things simple..

The elongated diffraction spots have become circular, which is due to the incident light being of a single wavelength. Additionally, some of the diffraction spots that were present when using white light have disappeared, and this is because the diffraction angle for the monochromatic light used is larger than the NA of the objective lens.

In this state, the original diffraction grating image is clearly visible as well. From this point, let's reduce the NA of the objective lens and observe how the diffraction spots and image change.

　Although the second order spots in the horizontal and vertical directions of the diffraction pattern are no longer present, the grating image still appears.

Further limiting the incident light, only the 0th-order and the 1st-order diffracted light pass through, and the grating structure is still visible.

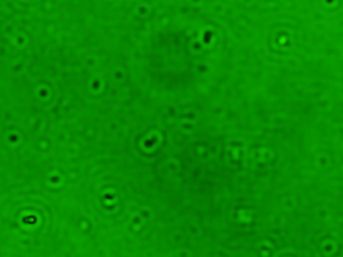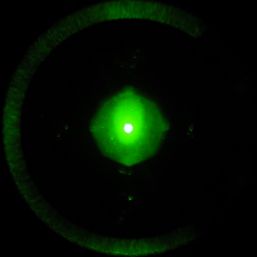
When the remaining t1st-order diffracted light are not allowed to pass through, the grating structure disappears. This change is dramatic. However, a closer look shows that the pattern of the grating structure changes as the number of passing spots decreases. The left figure includes the second order diffraction from the left, the center figure includes the remaining oblique diffraction, and the right figure includes only the first order diffraction from the top, bottom, left, and right. In the second-order case, a clear square grid is visible. Without second-order diffraction, the bright corners become rounded, and the grid appears less defined. The first-order-only image shows a structure resembling a collection of perforated circles.

This simple observation shows that in order to observe a periodic grating structure, the first-order diffracted light must be captured by the objective lens. From the equation for the period of the stripe structure and the diffraction angle ((3)), we can conclude that the finest interval d of periodic structures that can be observed with an objective lens of numerical aperture NA is

d=λ/NA …………(4)

Different wavelengths at the same grating spacing result in different diffraction angles.　Figure shows the diffraction patterns for 450, 500, 550, and 600 nm light. The diffraction patterns that were visible at 450 nm and 500 nm are lost at 550 nm and 600 nm.

We stitch the patterns at 450 nm and 600 nm together. The yellow circle corresponds to the NA of the objective lens.

For structures close to the resolution limit, diffracted blue light also enters the objective lens, but red light does not.

The images are adjusted to allow only blue light (from the blue part of the spectrum) to be captured by the objective lens. And in the next photo, blue and red filters are inserted on the illumination side.

As expected, the periodic structure shows better contrast with blue light than with white light, but not observed with red light.

Improvement of resolution by oblique illuminatio

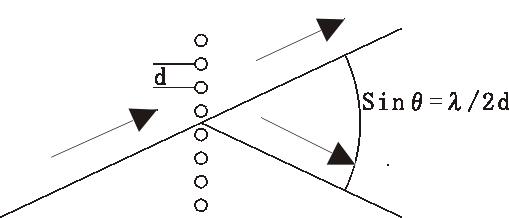
Fig. X  Diffracted light at oblique incidence, in which the diffraction angle is taken up by the objective lens to twice that at normal incidence.

As shown in this figure, when the illumination light is applied at an angle close to the NA of the objective lens, the first order diffracted light, which was not captured at normal incidence, can be captured through the opposite edge of the objective lens.

Fig. X: Image of oblique lighting with first order diffracted light in one direction (left)

　By introducing oblique illumination for zero-order light, the periodic structure is observed in the direction in which the first order diffracted light is taken in. However, the periodic structure cannot be reproduced in the direction in which only the 0th order light is taken in, which is perpendicular to the first order diffracted light. Therefore, it is observed as a lattice of vertical stripes even though the real thing is a square lattice.

When the 0th order light is incident obliquely, as shown above, the resolution in the direction of the oblique incidence is improved by up to twice as much as that in the direction of the normal incidence. This is a conventional technique called oblique illumination, which was a common illumination technique for research microscopes until the 1960s.

Change in image by restriction of incident light

 As shown above, when an image is formed only with diffracted light in a specific direction, an image different from the original structure is formed. In the example above, the period that appeared was the same as that of the original lattice, but when a specific diffracted light is selected by attaching a mask with a slit on the front surface of the objective lens, a different structure appears.

　The upper image shows the cross-grating image without the mask. The lower image shows the cross-grating image with the mask so that the vertical diffraction spots do not enter. As in the case of oblique incidence, only one direction of the diffraction spot is taken in, so it is not a cross-grating but a simple vertical stripe. The period of the stripe is the same as that of the cross-grating.

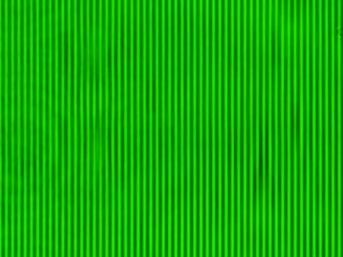
Next, the cross-grating is rotated by 45 degrees. When you look at the image without the mask, the spots diffracted in the diagonal direction of the cross-grating spread in the horizontal direction. Only the spot in the diagonal direction is selected by the slit in the lower image. As in the first image, it is a vertical stripe, but the period of the stripe is shorter than that of the cross-grating. Although it is different from the direction of the original cross-grating, you can understand what period is read from the original image rotated by 45 degrees.

The last one was rotated about 30 degrees. You can see which diffraction spot was picked up by looking at the image above. Because of the large diffraction angle, the period of the stripe that appeared is shorter than 45 degrees rotation. The contrast of the stripe is reduced because only the first order diffraction light was picked up.

Coherent Illumination and Incoherent Illumination

The discussion above is based on coherent illumination conditions, but most of the discussion on microscope resolution is based on incoherent illumination conditions. There are many discussions on incoherent illumination on the Web, so please take a look.

Objective lens back focal plane and Bertrand lens 

The figure shows the optical path when observing a double slit (the slit extends to the paper). The upper part of the figure is an ordinary observation, in which light from one side of the slit and light from the other side are formed as enlarged images on the image plane. In the double slit, interference occurs, and the light passing through the double slit repeats a light and dark pattern. In the figure, light traveling straight (zero order light) and light in the direction in which it first becomes bright (first order light) are drawn. For each direction, light passing through different slits is incident on the objective lens in parallel, so that the image is formed at the focal position (back focal plane) of the objective lens. By observing the image on this plane, an interference image of light and dark stripes can be observed.

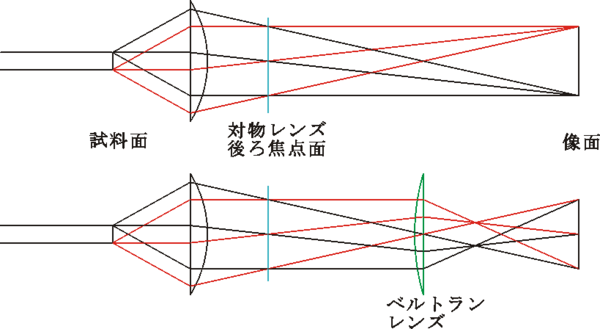
Fig X: Optical path diagram during normal observation and optical path diagram when a Bertrand lens is inserted

Some polarized light microscopes are equipped with a "Bertrand lens". When this lens is inserted into the optical path, the image of the back focal plane is formed on the normal image plane. The interference image can be observed directly. Even in a microscope without a Bertrand lens, the image of the back focal plane can be observed, although it is small, by removing the eyepiece and looking into the lens barrel. A large image can be observed by using a centering telescope (an eyepiece used for adjusting the ring of a phase contrast microscope). The image that can be observed with a Bertrand lens is called a "conoscopic image" in the industry. In contrast, the magnified image of a normal sample is called an "orthoscopic image".