“The Blind Girl” is a famous picture painted by an English painter John Everett Millais.　This painting features a beautiful rainbow that leaves a lasting impression on those who see it, making it a memorable work of art.

The painting depicts a tranquil, yet lonely scene of the English countryside. In the foreground, there is a path with two young female traveling performers seated on the grass. The elder sister appears to be blind, while the younger sister sits beside her. Both are dressed in poverty-stricken clothing.

A forest is shown in the background, and rising above the trees are two rainbows stretching across a dark, grayish sky. The colors of the rainbow are strikingly vivid, standing out in the otherwise somber landscape. The younger sister looks back at the rainbow, saying something to her elder sister. However, the blind sister, holding a hand organ on her lap, stares ahead blankly, unable to witness the beauty of the rainbow. The painting evokes a deep sense of pity, especially for the blind girl, who, amidst their poverty and misfortune, cannot even enjoy the beauty of the rainbow.

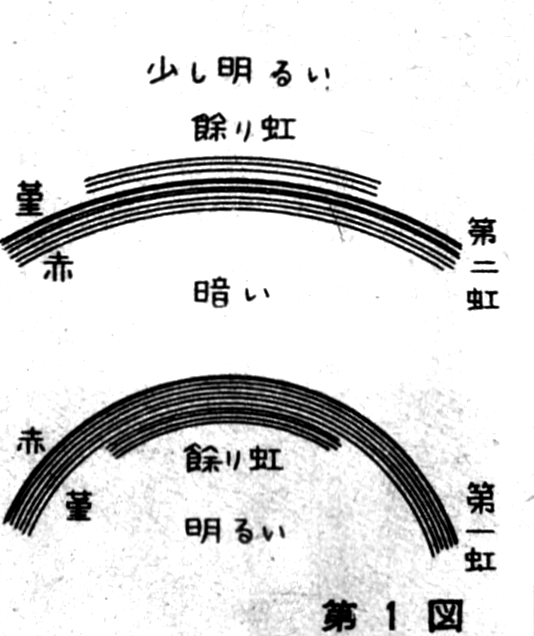
There is an interesting story regarding the two rainbows. Many people may know that when a bright rainbow appears, a larger, secondary rainbow often forms above it. When two rainbows are visible, the inner, primary rainbow is bright, while the outer, secondary rainbow is much fainter. This is how the rainbows are depicted in Millais's painting. However, there is another point worth mentioning, which concerns the colors of the rainbows.

Rainbows are commonly thought to display the seven colors of the spectrum. The phrase "seven colors of the rainbow" is familiar to everyone. While the colors of the rainbow and the spectrum are not exactly the same (a topic will be discussed later), the primary issue here is that the color arrangement of the first and second rainbows is reversed. In the first rainbow, red is on the outside, with violet on the inside, whereas in the second rainbow, violet is on the outside. This is true for all rainbows, and there is a reason for this reversal.

When Millais first painted the work, he mistakenly depicted the second rainbow with red on the outside, just like the first rainbow. This caused some debate, and after much discussion, he ended up repainting the second rainbow with violet on the outside. The version of the painting we see today is the corrected one.

The fact that the first rainbow has red on the outside, while the second has violet on the outside, is something taught in middle school science classes. Some might find it strange that such a simple mistake could be made. However, those who think this might not know as much about rainbows as they assume. The explanation of rainbows in textbooks only scratches the surface.

Next time you see a rainbow, take a good, careful look. First, although we often speak of the "seven colors of the rainbow," in reality, it's rare to see a rainbow where all seven colors—red, orange, yellow, green, blue, indigo, and violet—are present in that exact order. More commonly, the red and yellow bands stand out, while blue is often faint or even absent. In some cases, the red band is very faint, while the yellow and green bands are wider, and the red and violet bands are thinner. The idea of the "seven colors of the rainbow" is different from the seven colors of the spectrum. The phrase "seven colors" has led people to mistakenly believe that all rainbows contain the full sequence of spectral colors, but this is not usually the case. Anyone who closely observes nature even once will likely notice that even something as seemingly straightforward as the colors of a rainbow can provoke doubt. It is natural to question, as these things are not as simple as they seem.

Now, think back to a time when you saw a particularly vivid rainbow. You may remember seeing several weak and narrow rainbow inner part of the primary rainbow. These extra rainbows often appear doubly or triply in red and green. This phenomenon is not rare; it can be seen whenever the primary rainbow is strong. These arcs are an inherent part of the rainbow, and we might call them "supernumerary rainbows." Supernumerary rainbows can appear both inside the primary rainbow and outside the secondary rainbow, although they are often faint and can be hard to see in the latter case. However, their faintness does not mean they aren't there—they are just difficult to see due to their low intensity. Understanding rainbows also requires an explanation of these supernumerary arcs.

Some observers of supernumerary rainbows may also notice differences in the brightness of the sky. The sky inside the primary rainbow is brighter overall, and the sky outside the secondary rainbow, while darker, is still somewhat light. Meanwhile, the area between the two rainbows appears much darker, as if covered with a thin layer of ink. These variations in brightness are also part of the phenomenon of rainbows. Just as the beautiful colored rings of the rainbow are fascinating, so too is the difference in sky brightness. Beauty and prominence are subjective, human concepts, but from the standpoint of natural phenomena, the presence of even a single unexplained anomaly means we do not fully understand the phenomenon.

Additionally, there is an often-overlooked issue with the shape of the rainbow. Textbook explanations suggest that rainbows should be perfect circles with a consistent width. However, careful observation reveals that actual rainbows are sometimes elliptical or slightly distorted. The width of the rainbow can also vary, not only between different rainbows but even along the same rainbow. Some parts may be wider, while others are narrower. One explanation is that the state of the water droplets causing the rainbow changes depending on their location in the sky, affecting the shape of the rainbow. However, unless we can understand exactly how differences in the droplets affect the shape of the rainbow, this explanation remains incomplete.

I will now attempt to explain these various phenomena in order, so that readers can understand that the rainbow, often thought to be a simple and well-understood phenomenon as depicted even in middle school textbooks, is in fact far more complex.

Let's begin by explaining the concept of a rainbow as described in textbooks. A rainbow occurs when sunlight is reflected and refracted by raindrops, with the raindrops acting like prisms that break the sunlight into a spectrum. This is the principle behind a rainbow, and there is no deviation from this basic principle. However, since the raindrops responsible for the rainbow are spread across the sky, why does only a circular band of light appear instead of the entire sky lighting up? This is the question we will explore first. The issue of color will be discussed later. If sunlight were composed of just one color, the rainbow would simply be a circular band of that color. This can be confirmed through an experiment in which a monochromatic light, such as yellow light, is used to create a rainbow in a laboratory, resulting in a yellow rainbow.

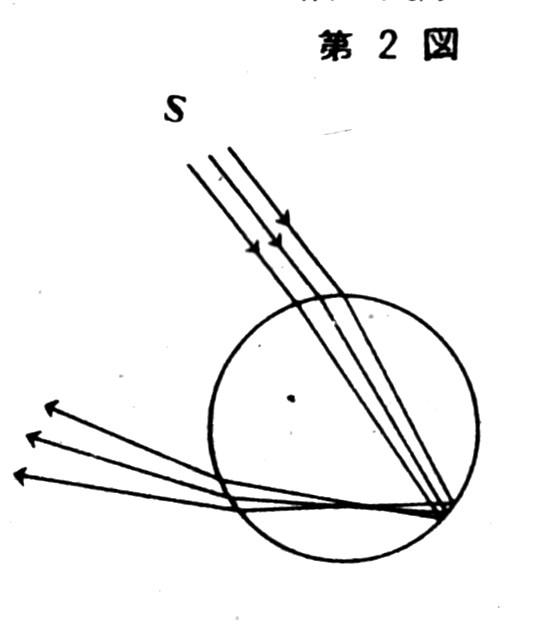
When sunlight hits a water droplet, part of it is reflected, but most of it is refracted and enters the droplet. The light is then reflected inside the droplet and refracted once more as it exits. Figure 2 illustrates the simplest case of this process. As shown in Figure 2, sunlight consists of parallel rays, but the light exiting the droplet is not parallel. If this were the only phenomenon occurring, no rainbow would form. Since raindrops are scattered throughout the sky, as shown in Figure 3, light refracted and reflected by droplets in all directions reaches the observer. Thus, the entire sky would simply appear bright.

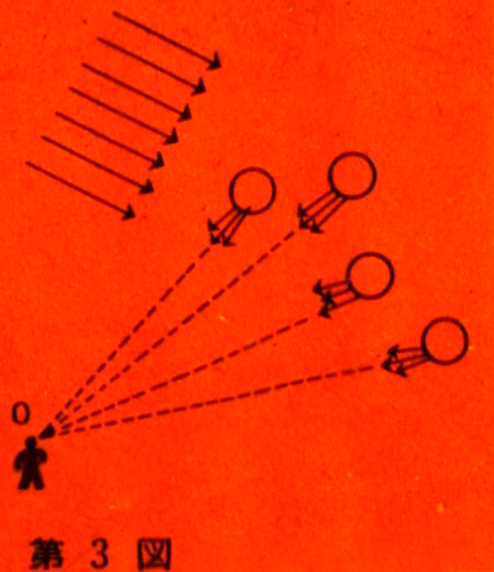
However, according to the theory of optics, there is a special characteristic when parallel rays of light are reflected and refracted by water droplets. Although the light emerging from the droplets is not parallel and spreads out, the way in which it spreads is not as depicted in Figure 3. Figure 3 was deliberately drawn incorrectly. 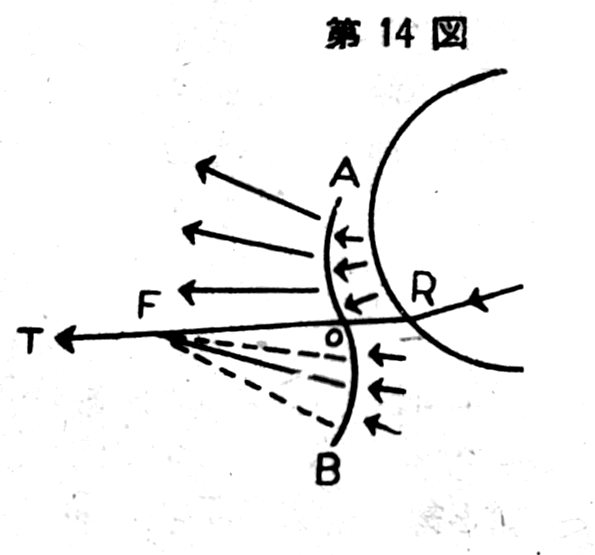When accurately illustrating the path of light inside and outside a droplet, it looks like Figure 4. In Figure 4, the ray of light SP strikes point P on the droplet’s surface and exits in the direction of RT. The other rays of light—such as rays 1, 2 above SP and 3, 4 below—also exit the droplet in the direction of R. At first glance, one might assume that rays 1 and 2 should exit above RT and rays 3 and 4 below it, but optics proves this is not the case. Thus, point P on the droplet’s surface is a special point. The significance of this special point lies in the angle at which light strikes the droplet’s surface. The angle between the sphere and the incident light is determined by the tangent plane at the point where the light strikes. When the angle between SP and the sphere is a particular value, the light exits in the direction of RT. Light rays in the same direction as SP, such as rays 1, 2, 3, and 4, strike the droplet at angles different from the special angle and are refracted upwards from the direction of RT. The rays of light exiting the droplet converge in the upward direction of RT and then scatter, so more light is concentrated in the direction of RT, making the light in that direction particularly strong.

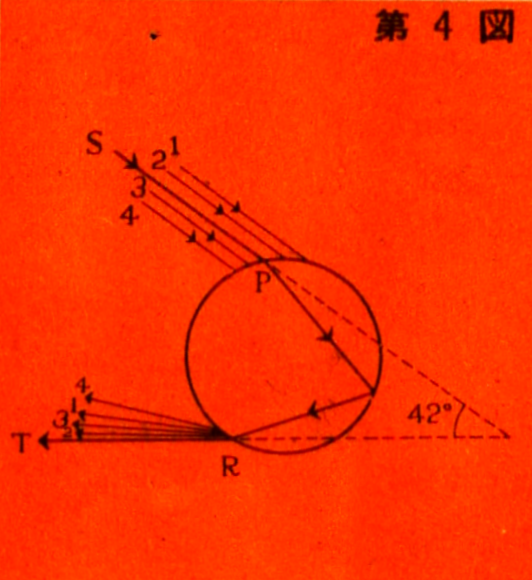
The direction of RT is a special direction. The angle between this direction and the initial direction of sunlight is determined solely by the refractive index of water and is independent of the size of the raindrop. Naturally, refractive indices vary depending on the substance, and they also vary based on the wavelength of light, i.e., the color of the light. When considering the average refractive index of water for the full wavelength range of sunlight (white light), the refractive index is 1.333. Calculating the angle between SP and the upward direction of RT in this case yields a value of 42 degrees. This is the angle for the primary rainbow. When we measure the angle of an actual primary rainbow, it is found to be approximately 42 degrees, thus confirming our explanation of the rainbow.

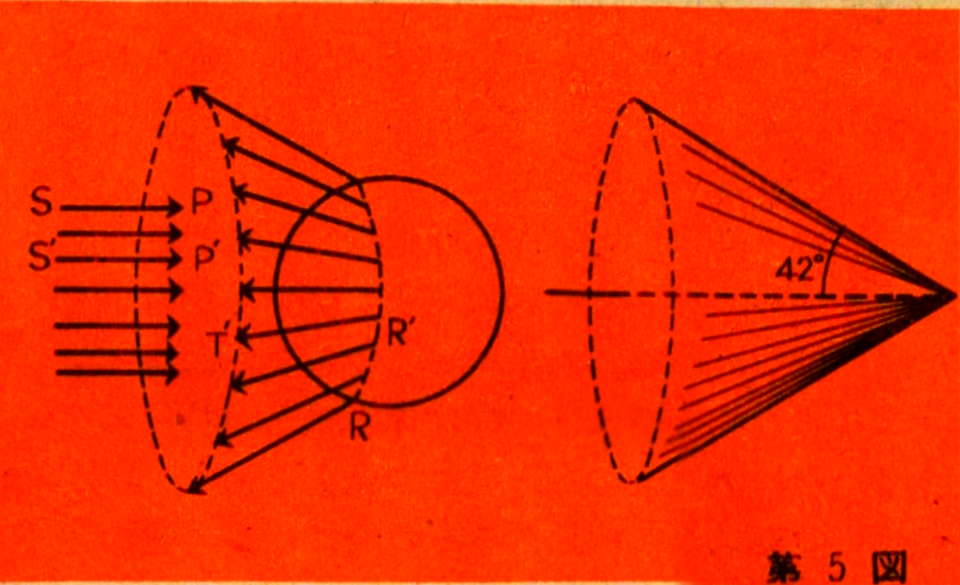
The 42-degree angle of the actual rainbow requires further explanation. The water droplet, which was illustrated as a circle in Figure 4, is in reality a sphere. Hence, the RT direction is three-dimensional, and as shown in Figure 5, the surface of the cone containing RT becomes the surface where the light is strongest. The 42-degree angle refers to the angle between the axis of the cone and the line formed by the cross-section of the cone's surface. Raindrops are scattered throughout the sky, and each of them sends light to the surface of the cone, as shown in Figure 5. 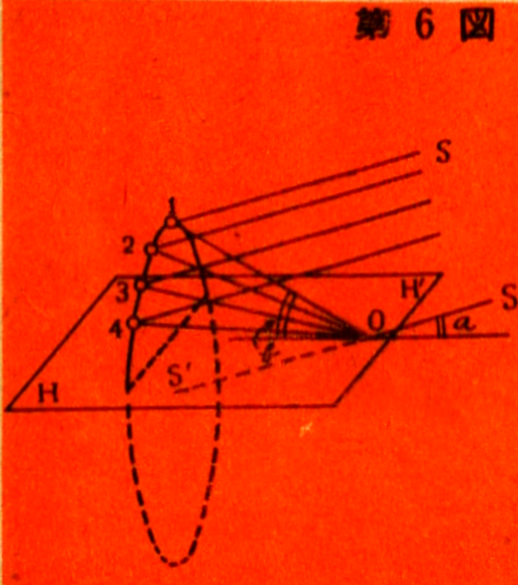This is why the human eye perceives a circular rainbow, as shown in Figure 6. In this diagram, H represents the horizon, O is the observer, and S is the direction of the sun. The light does not only come from the raindrops along the arc 1-2-3-4, but from all the droplets located on the surface of the cone with its apex at point O. The angle of the rainbow is the sum of the sun’s elevation angle (a) and the rainbow’s elevation angle (b). This has been consistently measured to be around 42 degrees, thus confirming our explanation of the formation of the primary rainbow.

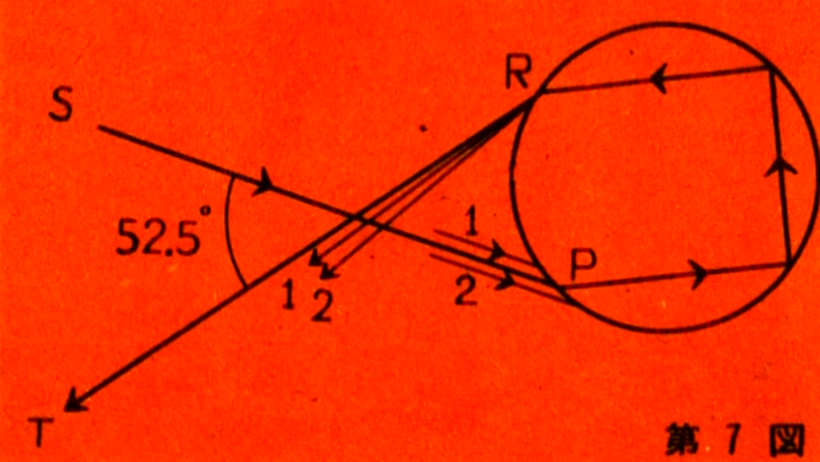
The secondary rainbow can be explained in much the same way as the primary rainbow. The secondary rainbow appears outside the primary rainbow, at an angle of approximately 52 degrees. It is formed by light that reflects twice inside a water droplet. Figure 7 illustrates the special direction in which the light exiting the water droplet becomes strong and the path the light follows. In this case, as with the primary rainbow, the light rays 1 and 2 above and below the SP line both exit above the RT line and then move to the underside of the RT line. According to the theory of optics, the light is strongest when the angle between the direction of the sunlight and the direction of the light exiting the droplet is 52.5 degrees. Within this angle, no refracted light emerges. Since this 52.5-degree angle matches the actual secondary rainbow, this explanation suffices for the secondary rainbow as well.

Now, one might wonder if there could also be a rainbow formed by light reflecting three times inside the droplet. In fact, such a rainbow does exist, and so do rainbows formed by four or five reflections. However, calculations show that both the tertiary and quaternary rainbows form in the direction facing the sun. Since the sunlight is so strong in that direction, the entire sky appears bright, obscuring the visibility of the rainbow. Calculations indicate that the quinary rainbow forms at roughly the same angle as the secondary rainbow, but the light is so weak that it is not visible to the human eye. The so-called "supernumerary rainbows" that occasionally appear near the secondary rainbow are entirely different from the quinary rainbow.

With this, we have explained the causes of both the primary and secondary rainbows. However, we have not yet addressed the issue of how sunlight is broken down into a spectrum, that is, how rainbows acquire their colors. Let us now move on to that explanation.

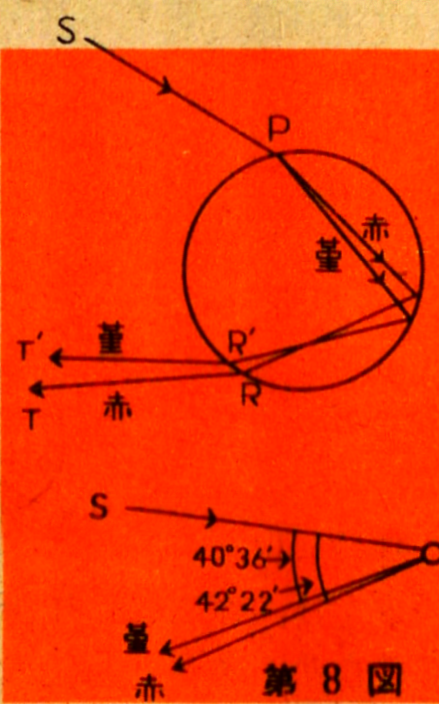
This explanation is relatively simple. Sunlight is a mixture of seven colors: red, orange, and so on. Of course, the seven colors are just representative; in reality, the colors change continuously from red to violet. For simplicity’s sake, we will refer to them as seven distinct colors. As mentioned earlier, the refractive index of water varies depending on the color of the light. For red light, the refractive index is 1.331, and as the color shifts toward violet, the refractive index increases, reaching 1.344 for violet light. In Figure 8, of the mixed light striking point P, the strongest red light emerges in the direction of RT, while the strongest violet light emerges in the direction of R’T’. 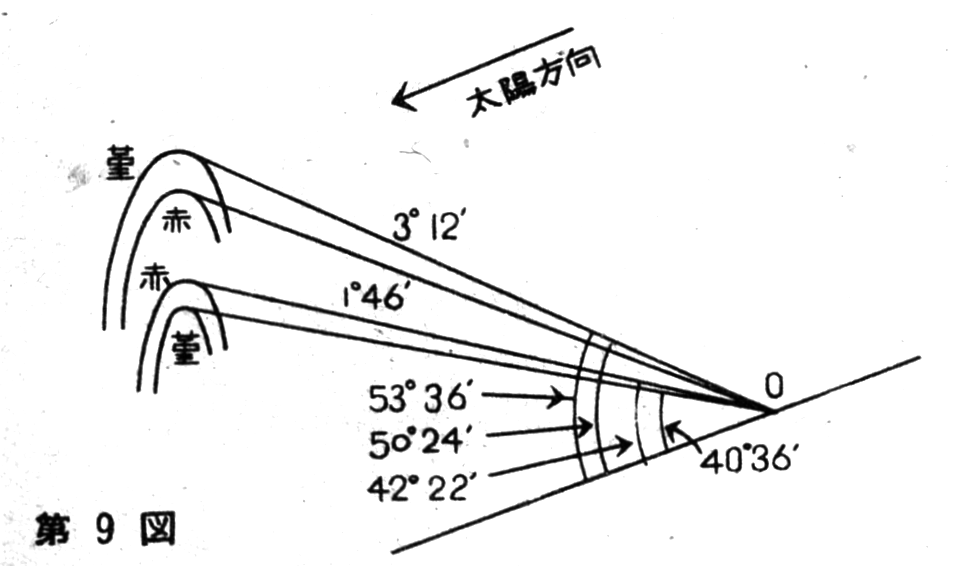According to calculations based on the refractive index, red light exits at an angle of 42 degrees 22 minutes, while violet light exits at 40 degrees 36 minutes. For the secondary rainbow, the red light exits at 50 degrees 24 minutes, and the violet light at 53 degrees 36 minutes. The relationship between the angles of red and violet is reversed in the secondary rainbow compared to the primary rainbow. This is why the outer edge of the primary rainbow is red, while the outer edge of the secondary rainbow is violet.

Because the refractive index changes in the order of the seven colors of the spectrum, this explanation implies that the arrangement of colors in any rainbow is always consistent, with the seven spectral colors appearing in the same order, and each color maintaining a uniform width across different rainbows. As shown in Figure 9, the width of the primary rainbow should always be 1 degree 46 minutes, while the secondary rainbow should be 3 degrees 12 minutes.

However, as previously mentioned, actual rainbows often vary in width, sometimes appearing wider or narrower. In fact, it is rather rare to see a rainbow that fully displays all seven spectral colors. This discrepancy makes it clear that the standard explanation found in most textbooks is insufficient.

The varying brightness of the sky, which I mentioned earlier, can actually be explained using the principles we’ve already covered, even though the differences in rainbow width and color arrangement present some difficulties. Let’s address the brightness issue first. In Figure 10, the light exiting a water droplet is represented by long lines for strong light and short lines for weak, dispersed light. Let’s consider the water droplets located inside the primary rainbow. Some of the weak, dispersed light coming from these droplets will align perfectly with the right angle and reach point O, as is clear from the diagram. Since there are countless such droplets inside the primary rainbow, this area appears uniformly bright. The same applies to the water droplets outside the secondary rainbow, with their light paths indicated by dotted lines.

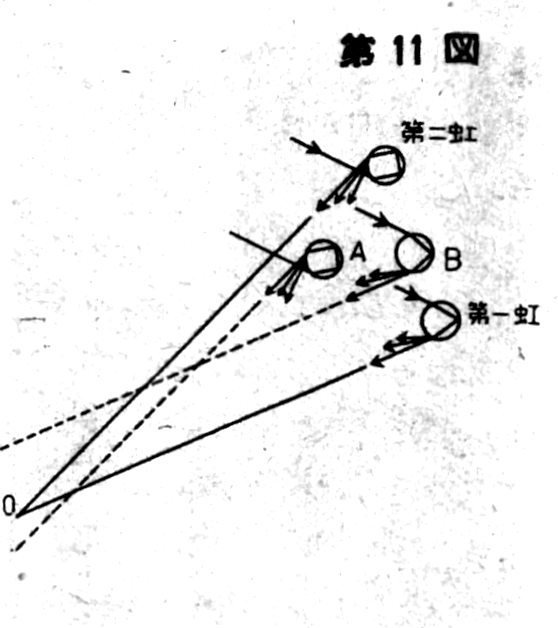
However, the light from the water droplets situated between the primary and secondary rainbows cannot reach point O. As seen in Figure 11, the light exiting droplets A and B, whether strong or weakly dispersed, is directed away from point O. As a result, no light from this area, including the weak dispersed light, reaches the observer’s eye through reflection and refraction, the key principles of rainbow formation. Therefore, this space between the primary and secondary rainbows appears much darker compared to other areas. The slight brightness present is due to the scattering of other light. This explains the variation in brightness across the sky.

Now we can move on to the remaining issues: explaining the width and color arrangement of rainbows, as well as supernumerary rainbows. At this point, we need to approach the problem from an entirely new perspective. The issue lies in the fact that up until now, all the light rays in our explanations have been represented as arrow lines. However, as everyone knows, light is actually a wave. 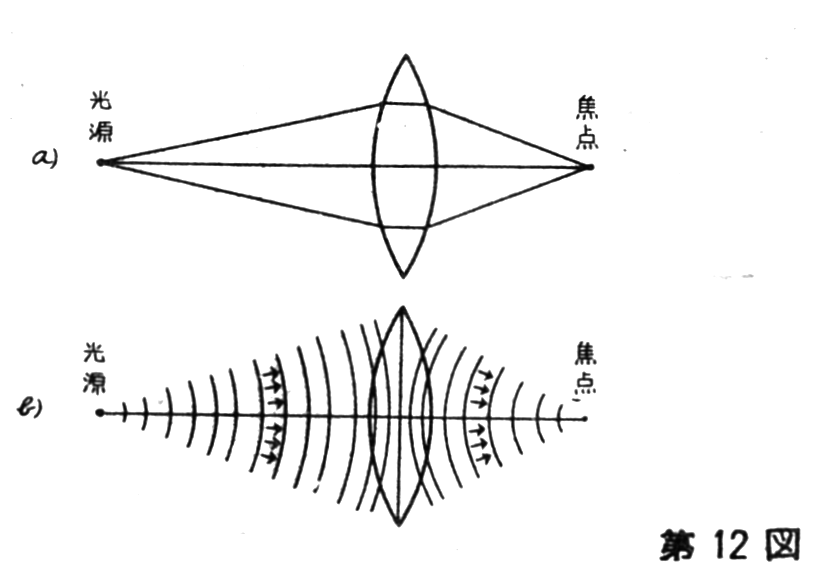Thus, to be precise, all light phenomena must be explained in terms of waves. For example, the phenomenon of light from a point source forming a focal point through a lens is usually depicted as in Figure 12(a). However, it is more accurate to represent it as in Figure 12(b). Even so, representing the direction of light waves with arrows, which are perpendicular to the wavefronts, is a simpler way to show the path of the light wave, and this method suffices in cases like the lens example. The wavelength of light is shorter than one-thousandth of a millimeter, so in most cases, the wave nature of light is not a major issue. However, when water droplets become very small, like the tiny droplets found in clouds, which are about one-hundredth of a millimeter, we must take the wave nature of light into account.

In the explanation of rainbow formation given so far, the size of the water droplets hasn’t been a significant factor. However, to address the remaining gaps in this explanation, we must now consider light as a wave. Supernumerary rainbows, for instance, can be well explained by the idea that interference occurs when light waves reflect and refract through small droplets. This interference is what causes supernumerary rainbows to form.

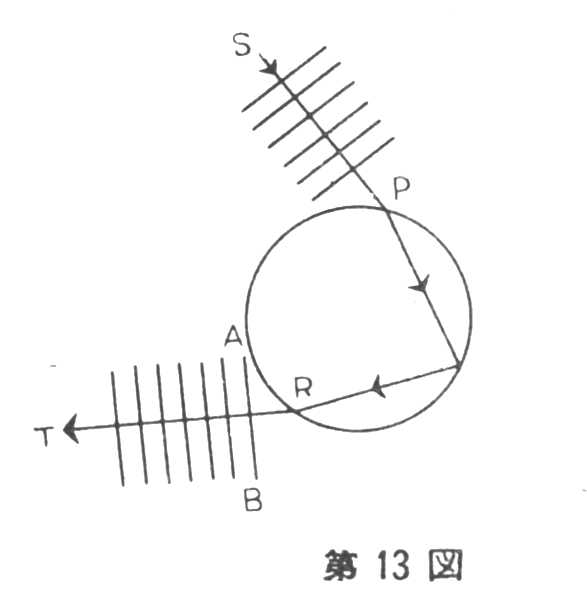
Let’s reconsider the formation of the primary rainbow by looking at light as a wave. If we examine only the top lines SP and RT from Figure 4 and overlay the wavefronts of light, it results in something like Figure 13. However, this alone reveals nothing new—it merely illustrates that the wavefronts are parallel and perpendicular to the direction of light travel.

Now, when the water droplets are small enough that we can no longer treat the wavelength of light as negligible compared to the droplet’s radius, a plane wave entering a droplet as parallel light rays will not emerge as a plane wave. The wavefront AB in Figure 13 transforms into the curved surface AOB in Figure 14, according to the wave theory of light. The curvature of the AOB surface is determined by the droplet's radius and the refractive index of water. As the droplet’s radius increases, this curved surface approaches a flat plane. Thus, the earlier explanations apply only when the water droplets are large. Between AO, the wavefront is convex, indicating that the light is diverging, while between OB, the wavefront is concave, meaning the light is converging. 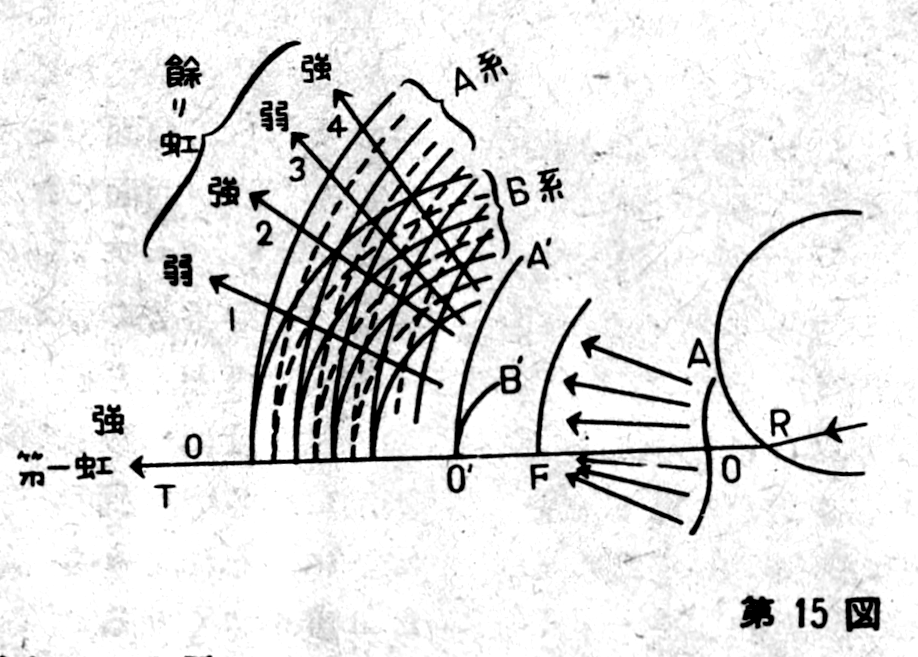The light in this region should focus at point F in Figure 15, and beyond F, the light begins to diverge again, with the wavefront becoming convex. As shown in Figure 15, just beyond the droplet, there are two wavefronts, O'A' and O'B', and interference accompanies these double wavefronts.

In this context, interference happens when two waves interact—when a crest overlaps with a crest, the light strengthens, but when a crest overlaps with a trough, they cancel each other out, weakening the light. This is the principle of light interference. In Figure 15, the waves from systems A and B are depicted with solid lines for crests and dotted lines for troughs. In the direction above RT, the crests from both systems overlap, strengthening the light. This is the forward direction, where light is particularly intense, corresponding to the conical surface at 42 degrees, as previously explained.

However, there are other directions, such as 2 and 4 in the diagram, where the interference also strengthens the light because the crests and troughs align (solid lines with solid lines, dotted lines with dotted lines). Conversely, in directions like 1 and 3, where crests and troughs from different waves overlap, the light is weakened. This interference causes two or three circular bands of light to appear just inside the primary rainbow, which are known as supernumerary rainbows. The light produced by interference weakens as it moves away from the focal plane, so typically only two or three such bands are visible, though in rare cases, up to six bands have been reported.

The above explanation provides a general overview of interference. More detailed calculations are required to determine the exact angles for directions 2 and 4 in Figure 15, as well as whether the direction O exactly matches the previously discussed 42 degrees. The British astronomer Airy calculated this and found that the angle for the primary rainbow is slightly smaller when calculated using wave theory than when using ray theory. Whether we treat light as rays or as waves depends on whether the wavefronts emerging from the droplet are planar or curved, and this curvature occurs when the droplets are small. Airy’s calculations revealed that in the case of large droplets, the angle for the brightest part of the rainbow almost exactly matches the previously mentioned 42 degrees, while for very small droplets, the angle is about 2 to 3 degrees smaller. Thus, by treating light as a wave, the size of the droplets becomes a critical factor for the first time.

This understanding also allows us to explain why rainbows are not always perfectly circular. If there are areas of large raindrops in the sky alongside regions with small cloud droplets, the rainbow can appear slightly irregular in shape without any problem.

The explanation above became quite complex, but up to this point, it only covers the behavior of light in one direction along RT, focusing on monochromatic (single-color) light. In reality, however, to explain a rainbow, one must consider the spectrum—red, orange, yellow, and so on—creating similar diagrams for each color and layering them with slight directional shifts, as shown in Figure 15. Only after doing this can we fully explain the rainbow. Yet, even with careful calculation, a crucial factor still remains unaddressed.

Supernumerary rainbows can always form within the primary rainbow. However, the angular distance between the primary rainbow and the first supernumerary rainbow is key. As mentioned before, the width of the primary rainbow is 1 degree and 46 minutes. If the gap between the primary and the first supernumerary rainbow exceeds this width, a strong, multi-colored primary rainbow will form, followed by a weaker supernumerary rainbow with seven colors. Usually, two or three such supernumerary rainbows can be observed. The interference theory shows that this gap narrows when water droplets are large and widens when droplets are very small. When the droplets are small, a fully formed primary rainbow is visible, followed by supernumerary rainbows inside it.

On the other hand, when the water droplets are relatively large, the gap between the primary and the first supernumerary rainbow becomes narrower than the width of the primary rainbow itself. In such cases, the red part of the supernumerary rainbow overlaps with the blue part of the primary rainbow. This raises the question of what happens when different colors of light overlap. This situation is entirely different from mixing pigments. For example, when red and green light overlap, the resulting light is perceived as yellow. Although the wavelengths of red and green light remain distinct, the human eye perceives them as yellow when they stimulate the retina simultaneously. If the intensities of red and green light are appropriately balanced, the resulting yellow light may appear nearly indistinguishable from yellow in the spectrum.

Such overlapping phenomena are surprisingly common in natural rainbows. When the red part of a supernumerary rainbow overlaps with the green part of the primary rainbow, that area appears yellow. Since the primary rainbow already has a yellow section just outside the green area, the yellow part seems unusually wide. This effect occurs when water droplets are relatively large. Beautiful rainbows seen after summer showers, for example, often exhibit this characteristic. Rainbows formed by larger droplets tend to be clearer and more vibrant. Think of the brilliant rainbows that sometimes appear after a summer shower—the red and yellow are striking, while the green and blue sections are less prominent.

The size of water droplets varies, leading to differences in the arrangement of rainbow colors. Therefore, it’s entirely natural for different rainbows to display varied color patterns. In fact, such variations should be expected.

At this point, we’ve explained most of the rainbow’s characteristics. When asked why rainbows form, most people will first mention refraction and reflection, which is a fine answer. For non-experts, knowing this much is commendable. However, this explanation alone falls short of addressing why some rainbows prominently feature only red and yellow, while green and blue are less noticeable. The failure to observe real rainbows closely leads to this misconception. Simply assuming that rainbows consist of seven distinct colors contradicts the spirit of science.

Nature is incredibly complex and full of mysteries. Even something as seemingly simple as a rainbow requires this level of explanation. In fact, many questions still remain. Only by steadily unraveling such intricate phenomena can we begin to truly appreciate the beauty of nature.

Some people might say, "Rainbows are just the result of spectral effects caused by the refraction and reflection of light in water droplets," and leave it at that. Such individuals, who don’t bother to observe actual rainbows, will never truly understand their beauty. They are like someone who has been blinded not by nature, but by their own reliance on superficial knowledge. While people naturally sympathize with someone who physically cannot see the beauty of a rainbow, it is also unfortunate when people blind themselves to the wonders of nature by failing to engage with it deeply.