屈折率分散の影響……異常偏光色・ベレックの限界……

　偏光顕微鏡の偏光色（干渉色）図表は、複屈折の値が波長によらず一定であるとして、作られたものです。 しかし、実際の物質の屈折率は波長依存性（屈折率分散）があり、複屈折にも分散が生じます。複屈折の分散が大きいと、分散なしの偏光色図表からの色調変化が生じ、変化が無視できない場合には異常干渉色となります。

　複屈折の分散は、コンペンセータを用いた複屈折測定にも影響を与えます。コンペンセータは分散の小さな材料で作られているため、分散が大きい試料では、観測波長全域での均等な補正ができないため、消光状態を正しく認識出来なくなります。

　屈折率分散が偏光色に与える影響と、ベレックコンペンセータを使って分散の大きな試料をの測定を行うときに注意すべきことを紹介します。

偏光色図表への屈折率分散の影響

　透過容易軸を垂直に配置した２つの偏光素子（クロスニコル）の間に複屈折物質を挟むと光が透過するようになります。複屈折物質が適当な厚みを持っている場合には、厚みに応じて特有の色彩（偏光色(Polarization color)）が見られます。偏光色は2つの偏光の光路差（OPD:Optical Path　Difference　またはRetardation)に依存して変化しますが、OPDが増加するときの色順と色味は薄膜干渉で膜厚が増加するときの色順と色味に類似しているためか干渉色(Interference color)と呼ばれています。しかし、光の干渉は同じ偏光方向の光の間でしか生じないものだし、偏光子を使わなくても見られる現象で、偏光板に挟んだ複屈折物質による着色は干渉とは異なる物理的機構により生じているものであすので、ここでは偏光色と呼ぶことにします。

一般に複屈折物質に入射した偏光は物質内を進行するにともない偏光状態は変化していきます。しかし、偏光状態を保ったまま物質内を進行する偏光状態が存在します。このような偏光を固有偏光と呼びます。物体に掌性がない場合は、任意の入射偏光は2つの直交する固有偏光に分けることができます。2つの固有偏光は、それぞれの偏光状態を保ち試料を透過しますが、それぞれの偏光に対する屈折率が異なっているため、屈折率で定まる光速は異なります。このため、出射時には2つの固有偏光の間にOPDが生じています。屈折率分散がない場合にはOPDは波長によらず一定値となります。一方、位相差はOPD値が同じでも、それが何波長分であるかは、波長に依存しますので、波長依存となります。つまり、出射時の2つの固有偏光の位相差には波長依存性があり、2つの固有偏光の合成により定まる出射偏光状態も波長依存性があります。このため、2枚目の偏光板を通過する光の量も波長に依存して変化し結果として色彩が生まれるのです。

偏光色図表

　OPDの増加にともない、偏光色は黄色→濃赤紫→青.→黄色→赤紫→緑と変化していきます。縦軸にOPD、横軸に試料の厚みをとり、それぞれのOPDでの色彩に彩色した図を偏光色図表（干渉色図表）といいます。縦軸がOPDなので、横軸方向にはOPDが一定で偏光色には変化がありません。偏光色図表の色味は、どのようなスペクトル分布の照明光を使っているかによって、微妙に変化するはずです。以下には、CIE-A、D50、D65光源を用いた偏光色図表を示します。

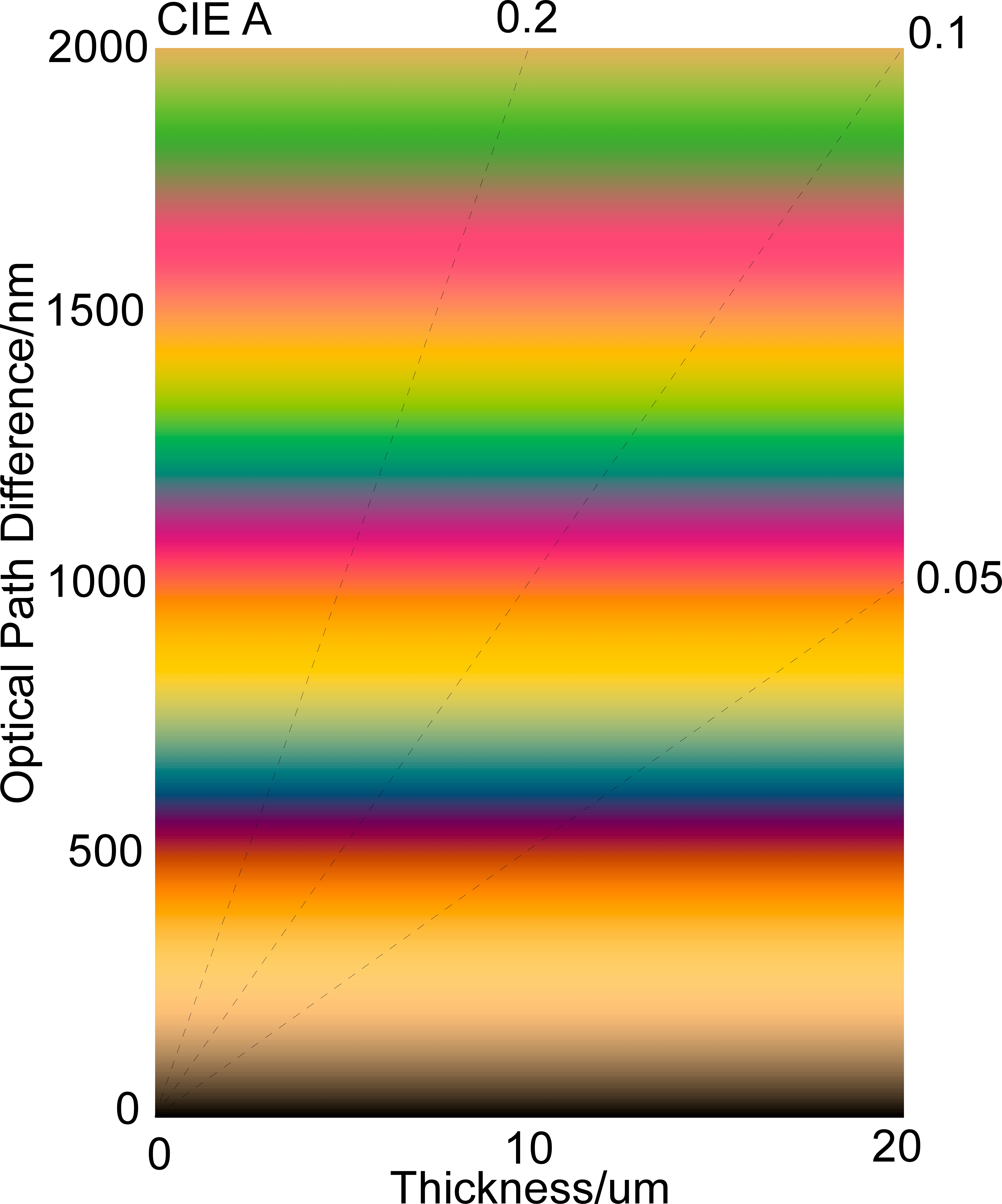
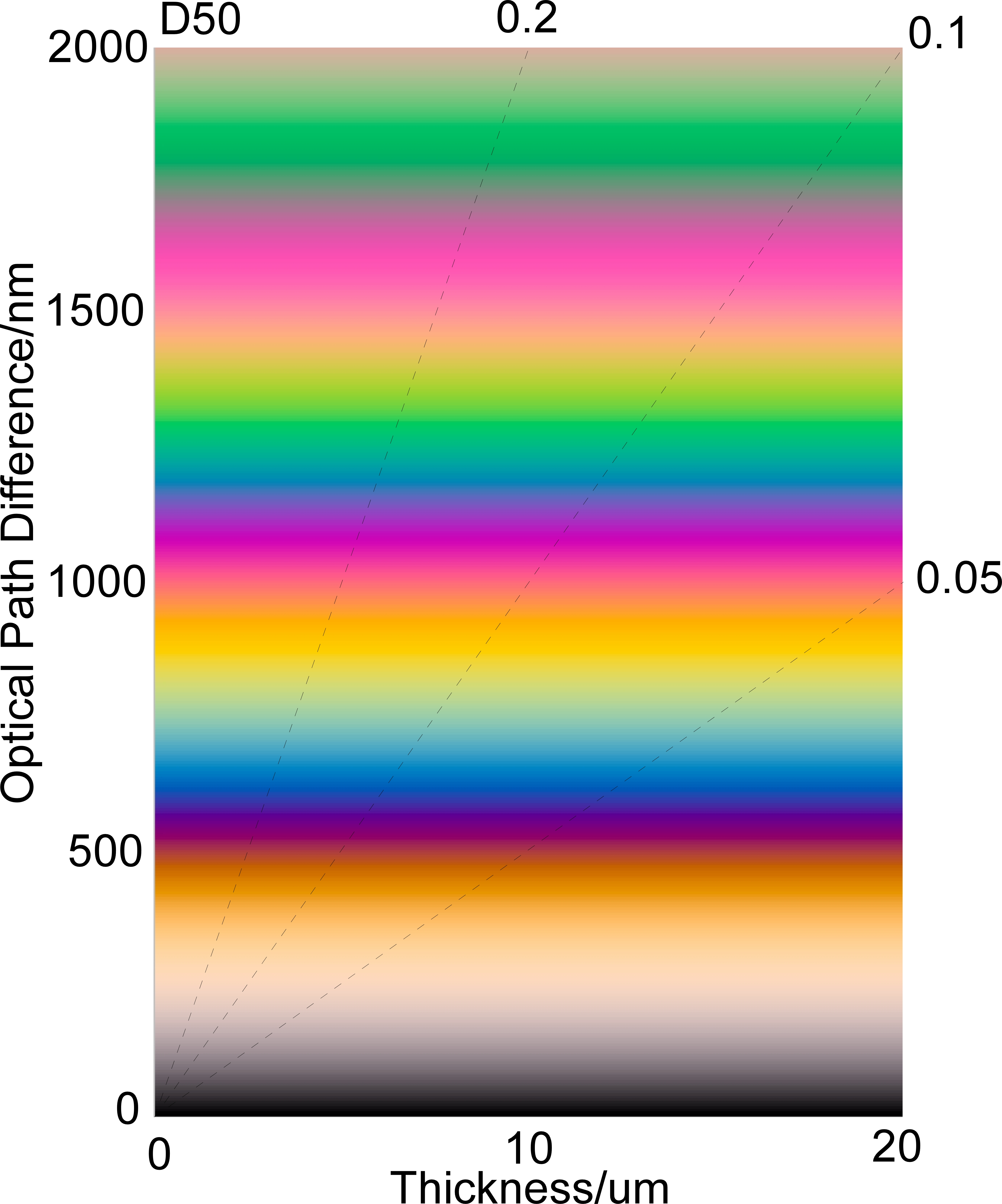
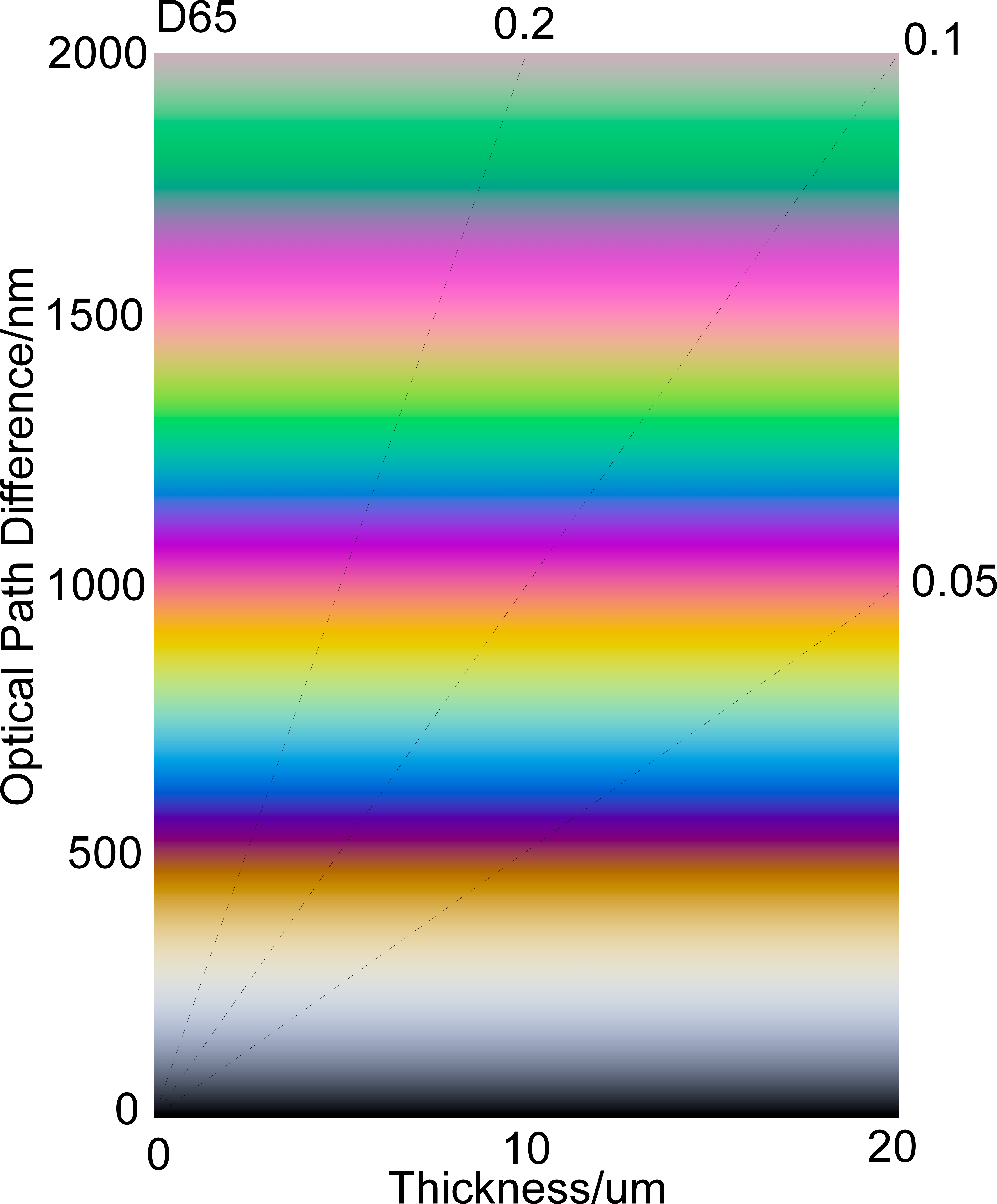
Fig. 1　偏光色図表（上からCIE-A、D50、D65)

　偏光色図表には一連の斜線が書き込まれています。斜線には、それぞれ、0.05とか0.1といった数値が書き込まれていますが、これらの数値は複屈折の大きさを示すものです。複屈折の大きさに試料厚を掛け合わせたものがOPDですので、試料の厚みが既知なら、偏光色に対応する部分を通過する斜線から、複屈折が見積もれますし、複屈折が吉なら、偏光色から試料の厚みが見積もれます。

　偏光色図表はOPD値が1500nmまで示されているものが多いようです。偏光色図表を見ても分かるように、530nm付近の赤紫は1000nm付近の赤紫より濃い色をしています。OPDが大きくなると、色彩が淡くなっていき、OPDが大きい極限では無彩色のグレーとなってしまいます。このため、色彩が明瞭に見られる1500nm程度の範囲までの図となることが多いのだと思います。

　昔の書籍では偏光色図表は手彩色のものが使われたりしていましたが、パーソナルコンピュータが発達した結果、OPD値ごとにスペクトルを計算して、ディスプレイやプリントの色彩を計算して偏光色図表を作成するようになっています。コンピュータを使うと、手彩色では困難だった、縦軸に試料厚、横軸に複屈折をとった、2次元の偏光色図表なども作成できます。

 

複屈折の分散の影響

　上に記したように実際の物質の屈折率には波長依存性（分散）があり、複屈折の値も波長に依存します。複屈折の分散が大きいと、偏光色の色調が分散無しのものから有意に変化してしまいます。標準的な偏光色図表とは異なった色彩の偏光色を異常偏光色といいます。異常偏光色の原因としては、屈折率分散のほかに元の物質の着色もありますが、ここでは、元の物質は可視領域で、ほぼ無色である場合のみを扱うことにします。

　複屈折の分散により異常干渉色となる目安として、坪井の本には＠による複屈折のアッベ数とも言うべき指標が紹介されています[1]。

　この指標値はD線に於けるΔｎが同じならC線とF線でのΔｎの差が小さい程大きくなります。もし分散がなく、屈折率が波長によらず同じ値なら、この指標値は無限大になります。この指標値が10程度以下になると、標準的な偏光色からのずれが目立つとされています。液晶試料の分散データより、指標値を計算すると、５CBで7.2、MBBAで4.5になります。いずれも異常偏光色の領域になっているのです。

　個々の物質については、屈折率の波長分散があれば、その物質に即した偏光色図表を描けます。のちほど、５CBとMBBAの異常偏光色図表を示しますが、その前に、指標値の変化にともない、偏光色がどのように変化していくかを示した図表をお目にかけます。

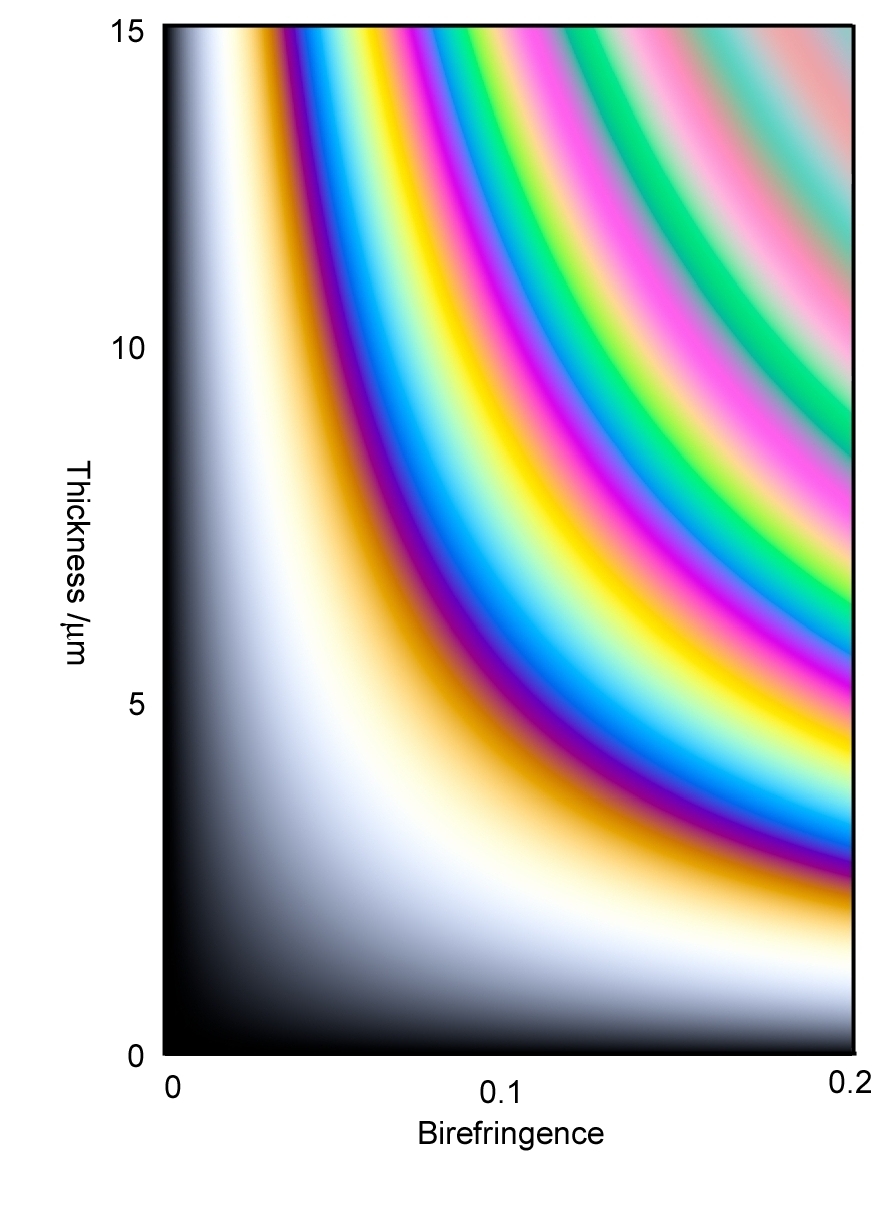
　横軸をΔν、縦軸をある波長でのOPDとした図を描こうとしているのですが、Δν値を定めても、それによって分散が一つの曲線に定まるわけではありません。そこで、一つの仮定として、分散がコーシーの分散式に従い、また、波長の4乗に関わる係数Bが0であるとして分散を求めて、それを用いてOPDを計算して偏光色図表を描くことにしました。作製したものを図２に示します。なお、分散のために波長ごとにOPD値が異なってしまいますので、縦軸のOPD値はD線での値です。

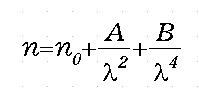
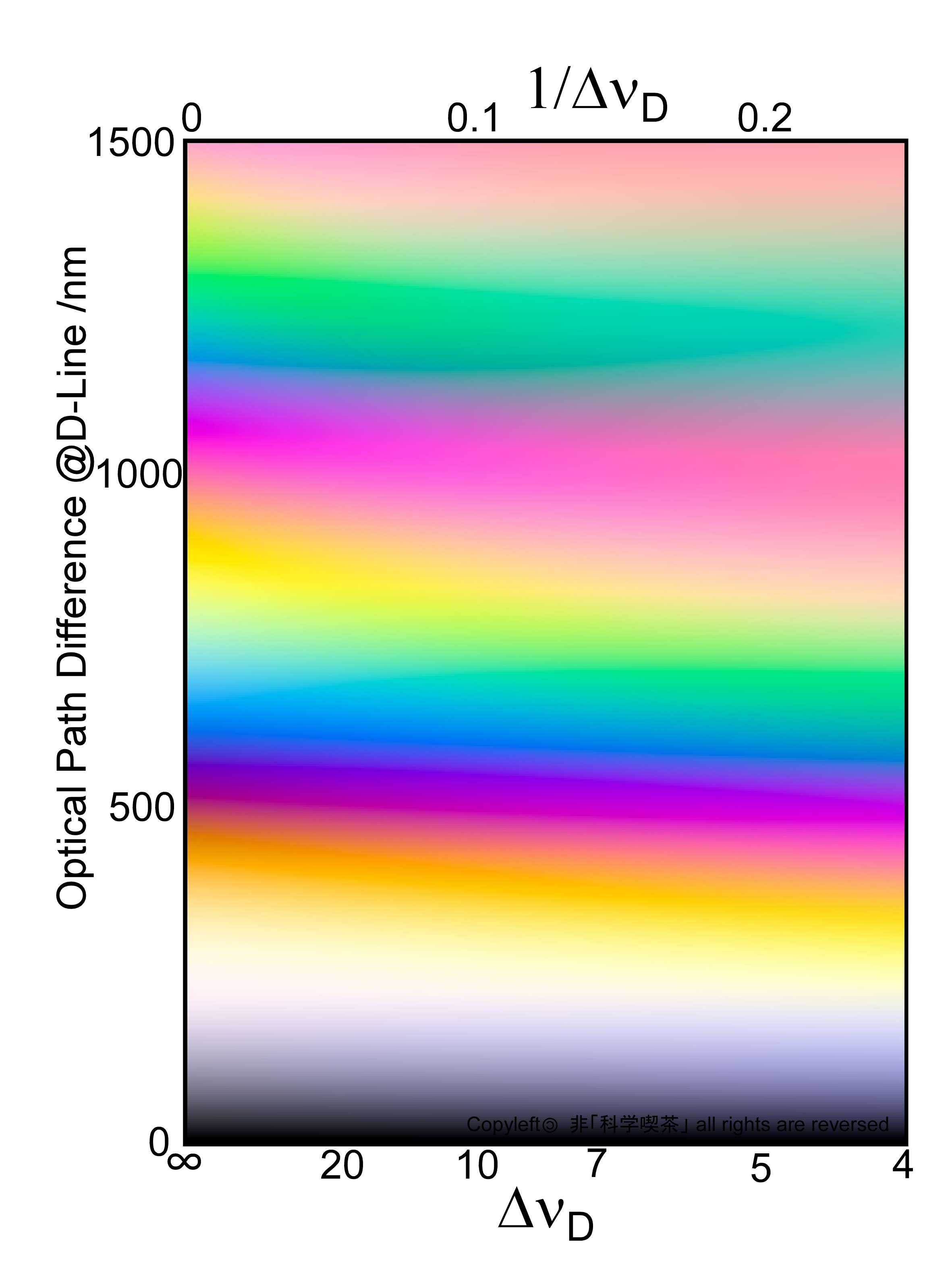
Fig. 2 複屈折分散の影響をいれた偏光色図表

　図の左端は分散がない状態で、通常の偏光色になります。OPDが750nm程度の水色の部分を左から右に見ていくと、分散がない場合の水色から、分散が大きくなると緑色へと変化していきます。分散がない場合には緑色はOPDが1000nmより大きいところで初めて見られる色ですので、分散の大きな試料で緑いろの色調からOPDが1000nm以上あると見積もってしまうと、複屈折を過大に評価することとなります。

ネマチック液晶５CBとMBBAの偏光色図表

　コーシーの係数がわかっている物質に関しては、その値を用いた偏光色図表を作ることができます。幾つかの液晶材料についての屈折率の報告[２]　のデータを用いて、５CBとMBBAの2種類の液晶材料のネマチック相について偏光色図表を描いてみることにしました。両方とも有名な液晶化合物で、５CBは無色の物質であるのに対して、MBBAは吸収が可視領域に及んでいて淡い黄色の物質です。吸収がより長波長まで伸びているので、屈折率の分散もMBBAの方が大きくなります。

　ネマチック相では液晶の内向秩序度が温度依存して変化するため、配向秩序度に依存する複屈折も温度依存性を示します。上記の論文には複数の温度におけるコーシーの係数が記されているので、複数の温度での偏光色を図にまとめることにしました。

　図3は５CBの、図４はMBBAの3つの温度における偏光色を示した図表です。縦軸はセル厚ｔしていますが、分子はセル界面に平行になっているとの仮定の下での値です。横軸はデータのあった3つの温度を使っています。

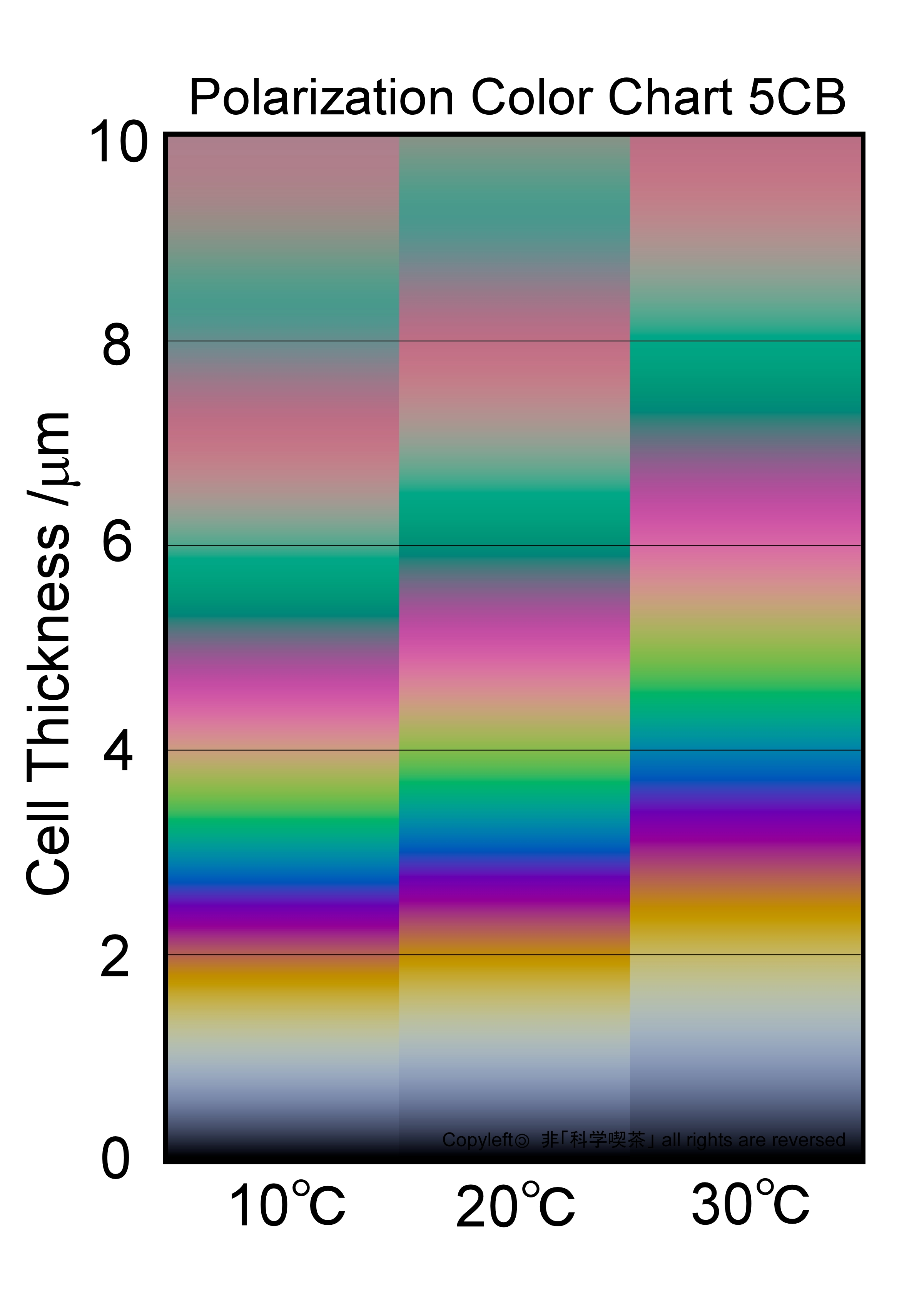
Fig.3 ５CBの偏光色図表

Fig. 4 MBBAの偏光色図表

• [1]　偏光顕微鏡　坪井誠太郎　岩波書店(19@@) P.@@.
• [2] Dispersion Properties of Refractive Indices of Nematic Liquid Crystals, R. Yamaguchi and S. Sato, The Journal of Institute of Electronics, Information and Communication Engineers C Vol J71-C No.9 PP1241-1247(1988).(Japanese)
  

ベレックコンペンセータの補償限界

　ベレックコンペンセータはOPD量可変の位相差板で、偏光顕微鏡のスロットホルダーに装着して、試料のOPD測定に用いる器具です。ベレックコンペンセータは光学的１軸性物質で作られた平行平板で、光軸は平板に垂直方向になっています。このため、顕微鏡の光軸に対して面を垂直に光路に入れてもOPDは生じませんが、平板を顕微鏡光軸に対して傾けると角度に応じたOPDが生じるようになります。 スロットホルダーは偏光子/検光子の光軸に対して45度方向に作られています。
Fig. 5 ベレック型コペンセータ（オリンパスPOS用）

　写真で示したものはオリンパスの旧型用のもので、オリンパスPOS型用のものです。最近の機種ではDINのスロットホルダー規格のものが汎用性があるように思います。 　

  　ベレックコンペンセータには0〜60程度の範囲目盛りがふってあることが多く、30付近でコンペンセータの光軸が顕微鏡の光軸と平行になり、コンペンセータのOPDは０となるように作られています。まず、試料の光軸を偏光子/検光子から45度に調整します。位相差板スロットにベレックコンペンセータをいれて、ベレックのOPDが０の状態からノブを回します。ノブを回すと試料の偏光色が変化していきます。もし、色調の変化がOPDが増加する方向でしたら、試料を90度回転します。OPDが減少する方向でしたら、そのまま目盛りを回転し、試料のOPDをコンペンセータのOPDが打ち消すように調整してその時のコンペンセータの目盛りを読み取ります。続いて、30をはさんだ反対側でOPDが打ち消す目盛りを確認します。読み取った、2つの値を用いてコンペンセータに付属のデータを使って試料のOPDを求めます。 　

　コンペンセータには、方解石のような負の１軸性結晶が使われているものもあれば、フッ化マグネシウムのような正の一軸性結晶が使われているものもあります。このため、回転する方向に対して屈折率が大きくなるか小さくなるかはコンペンセータにより異なっています。どちらのタイプであるかは、コンペンセータに記してあるＺ’軸方向を見れば確認できます。 　

　コンペンセータ単体でノブを回すと、視野内で帯状に色が変化していきます。コンペンセータの作り出すOPDは視野内で均一ではありません。コンペンセータを使う時は、十字線の入った接眼レンズを用いて、視野の中心で補償を確認するようにします。なお、色調が帯状にと記しましたが、OPDが小さい時には線ではなく横に広がったぼんやりした点状となります。下の図6にあるように、OPDが小さいとコンペンセータの傾き変化に対してOPD変化が少ないので、測定感度はよくありません。

　オリンパス（現エビデント）のWeb上では測定範囲が1600nm程度までのものと10000nm程度のベレックコンペンセータが掲載されています。また、ニチカのWebでは約1800nmまでのものが掲載されています。有機物は後述するように、複屈折の分散がコンペンセータの素材とはかなり異なるため、OPDが大きくなると補償は完全からほど遠い状態になります。このため、有機物を使う限りは、10000nmまで測れるものの出番は少ないだろうと思います。

コンペンセータの回転角とリタデーションの大きさ

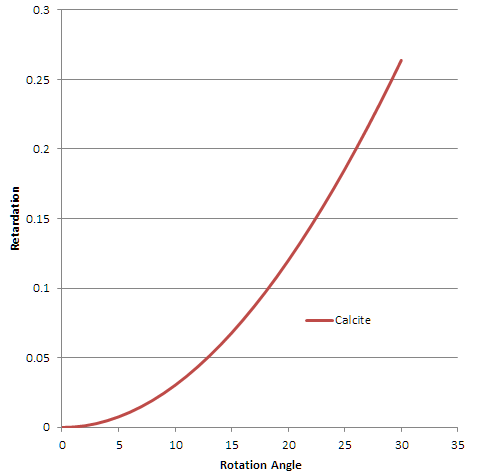
Fig. 62 回転角とリタデーション

図6にコンペンセータの回転角とOPDの関係を示します。OPDは回転角に対して線形に変化するのではなく、下に凸の曲線です。この図は下に示す3つの式の一番初めのもので作成したと思いますが、他の2つでも曲線は実質的に重なります。最初の式は、旧オリンパスのWebサイトに掲載されているもので以下の形をしています。

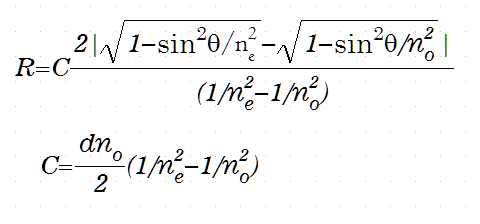
ここで、neとnoはコンペンセータに用いている複屈折物質の異常光と常光の屈折率です。

坪井の「偏光顕微鏡」の中にある、OPDと入射角の関係式で次の形をしています。

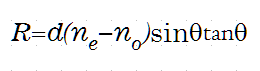
オリンパスの式に比べると随分と簡単なものですがカルサイトの屈折率をいれてグラフを描いてみると、オリンパスの式と同じ曲線が得られます。

上記の式に対して、物理的な背景なしの次のような実験式でも上記の２つの式と重なる曲線が得られます。

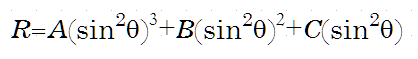
この式なら、ベレックコンペンセータに使われている複屈折物質が何であるかが分からなくても、パラメータ値を決めることが出来ます。 　

　ベレックコンペンセータには、それぞれのコンペンセータ毎の補正係数が記されたデータシートが添付されています。コンペンセータの係数はコンペンセータの板厚に依存するため、コンペンセータ毎の係数は異なっているようです。補正係数のデータシートは、対応する製品にのみ有効なので、異なる組み合わせで使わないように気をつける必要があります。

データシートが見当たらない場合には、自分で係数を決める必要があります。この時、役立つのが上の3番目の式です。係数を決める手法は単純なもので、OPDが既知の位相差板をデータシートのないコンペンセータで測定して、その時の読みから、実験式のパラメータを定めます。３番目の式では未知数が3つあるので、複数点での測定が必要となります。 OPD既知の位相差板としては、偏光顕微鏡に付属のλ/4板や鋭敏色板(R=530nm)を用いることが出来ます。OPDが小さいと、消光が線ではなく点に近くなったり、黒い領域の幅が拡がったりするので、λ/4板より鋭敏色板を用いた方がよい精度で測定できます。位相差が複数あれば、それらを重ねることにより異なったOPDの測定対象を作り出すことができます。

屈折率分散の測定への影響

コンペンセータの素材と、測定対象とで複屈折の分散が異なる場合には、波長により補正の程度が異なってしまいます。このため、ある波長でOPDの補正が行われていて完全な消光状態になっていても、別の波長では補正がきちんとできていないために光が漏れてしまうことになります。可視領域全域で消光状態にすることはできないのです。試料のOPDが小さい場合にはずれも大きくないので、疑似的にではありますが、消光状態を見出すことができますが、OPDが大きくなると、ずれが大きくなってしまい、疑似的にでも消光状態をきちんと見いだせなくなります。どの程度のOPDまで測定できるかは、ベレックコンペンセータに用いられている物質の複屈折分散と、対象試料の複屈折分散がどの程度異なっているかによります。

  ベレックコンペンセータの補償板は方解石などの無機物で作られているため、分散が大きくは異ならない無機物を対象とする場合には、リタデーションがそこそこの値でも十分に補償が行われて、消光状態が観測できます。図７にナトリウムのD線でリタデーションが2000nmの水晶板を、方解石のコンペンセータを使って補償した時の色調変化のシミュレーションを示します。

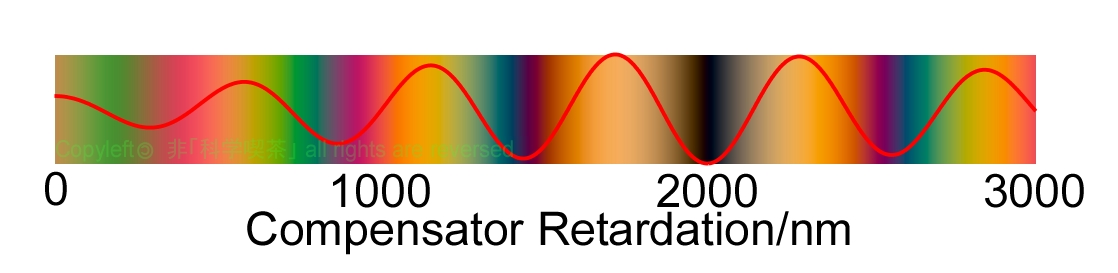
Fig. ７ OPD2000 nmの水晶を方解石で補償したときの偏光色シミュレーション

図からも分かるように、2000 nmで色調は黒くなりもっとも暗くなっています。消光した読みから両側に500nm程度ずれたあたりは、鋭敏色の赤紫が少し非対称に見えている。非対称性は、水晶と方解石の分散が少しばかり異なっていることから生じています。 　

続いて、図８に５CBのネマチック相を対象に方解石のコンペンセータで補償を試みたシミュレーションの結果を示します。図左の数値は図７と同様にナトリウムのD線でのリタデーション値です。

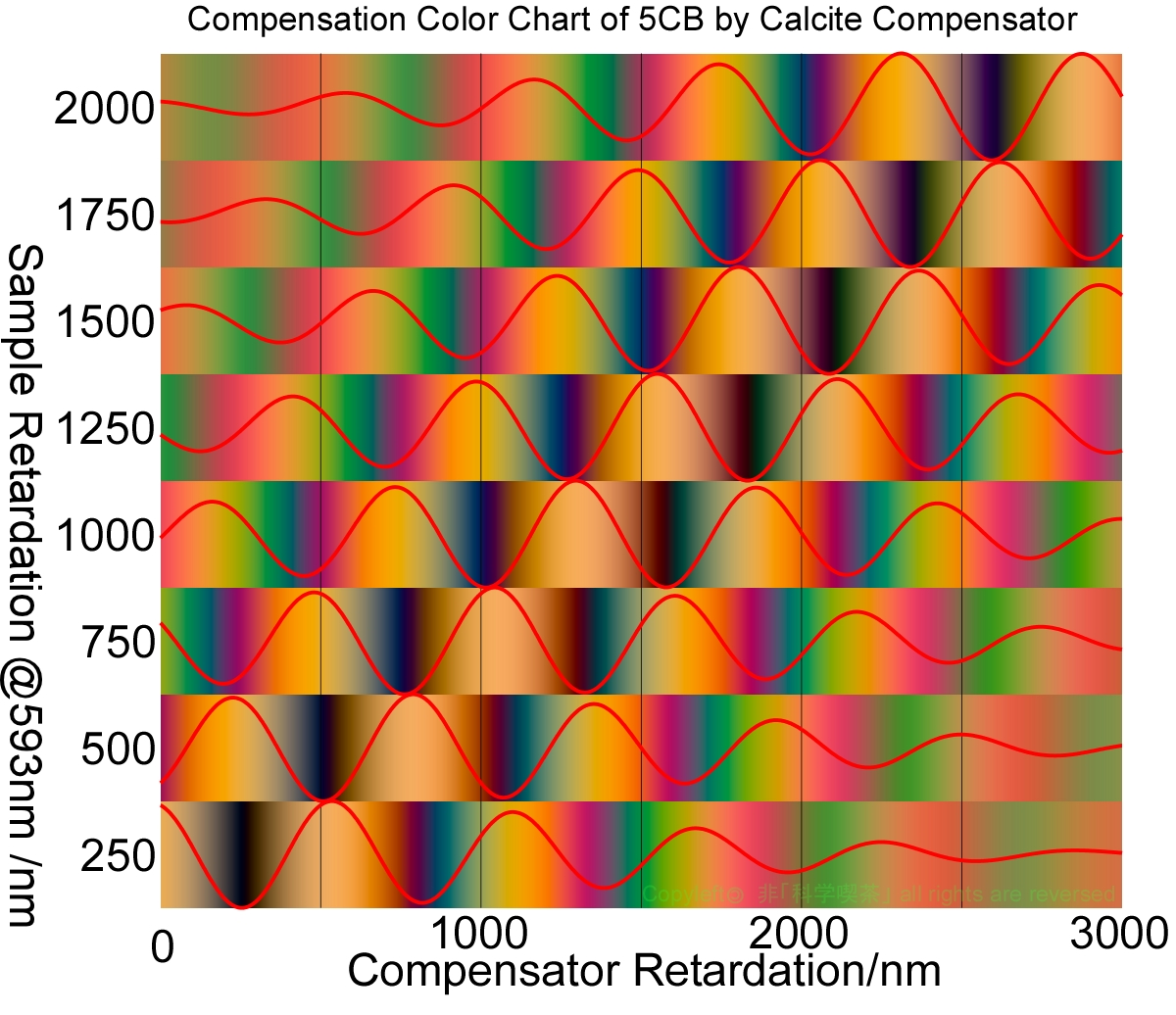
Fig. 8　５ＣＢを方解石で補償したときの偏光色シミュレーション
　試料のOPDが750 nm程度までは、正しい値のところがもっとも暗くなっているようです。しかし、OPDが1000 nmに達すると、1000 nmの他に1500 nmを越えたあたりの極小値も同様に暗くなってしまい、どちらが正しい読みかの判断は困難になります。さらに、1250 nmを越えると、正しい値より、それより一つOPDが大きいところの極小の方が暗くなっており、目視では完全に読みを誤るであろう状態となっています。

　単色フィルターを使うと原理的には、複数ある極小の明るさが同じになるはずです。しかしながら、通常の偏光顕微鏡に付属している緑色フィルターは、透過波長域が狭くはなく、、その範囲での分散の影響が出てしまい、正確な測定は困難です。図9はニコンの偏光顕微鏡に付属している干渉タイプの緑色フィルターの透過スペクトルを用いたシミュレーションですがＯＰＤが大きくなると、本来の補正値より一山先の谷で強度が最小になってしまっています。

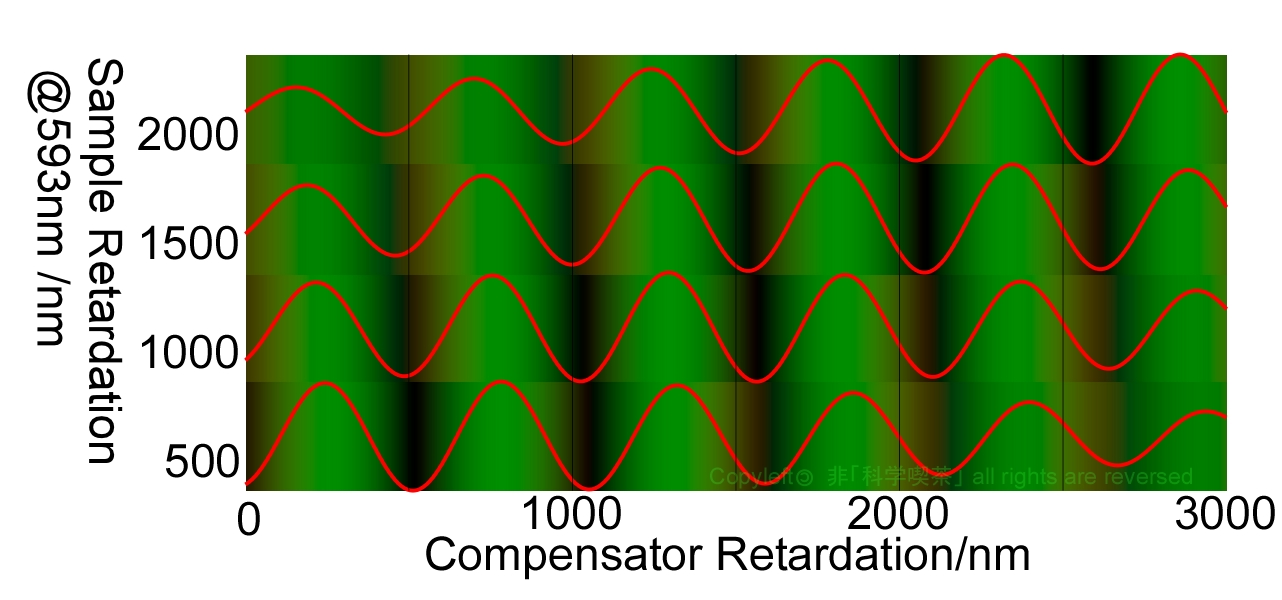
Fig.9 Compensation of 5CB with green filter 　

　５CBよりも複屈折分散が大きいMBBAでは、状況は更に悪化します。図１０にMBBAのコーシー係数を用いて計算した分散を使ったシミュレーションの結果を示します。MBBAの場合は、ＯＰＤが500 nmで本来の位置と一山先の谷が同じ程度の明るさになり、750 nmではそちらの方が暗くなってしまっています。ＯＰＤ1750 nmでは、２山先の谷がもっとも暗くなってしまっています。MBBAはシッフ塩基を含み僅かに黄色に着色しており、同じようにシッフ塩基を含み、着色のある材料のリタデーションをベレックを使って評価する時には、かなりの注意が必要となります。

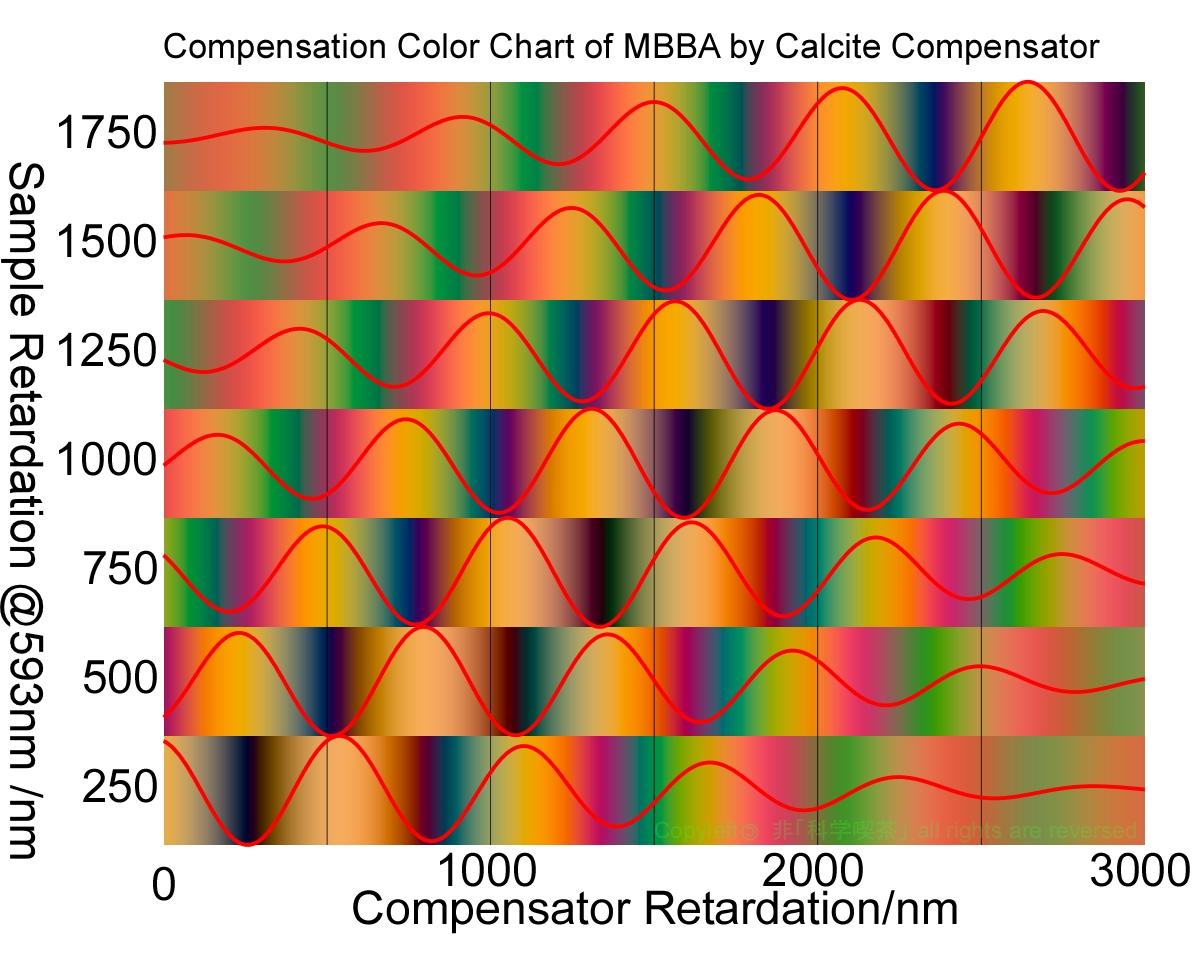
Fig 10. Compensation of MBBA by Calcite