顕微鏡の分解能

　凸レンズの結像倍率は、レンズから物体までと、像までの距離の比となる。物体をレンズの焦点位置に近づけていくと比は制限なく大きくなる。対物レンズの焦点距離が短ければ実用的な鏡筒長の顕微鏡で1000倍どころか、1万倍以上の拡大だって可能ではある。実際、やたら高い倍率を誇っていたマイクロスコープもあった。

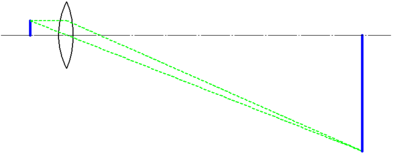
図：幾何光学的な像の拡大。拡大率はいくらでも大きくなる。

開口数NA

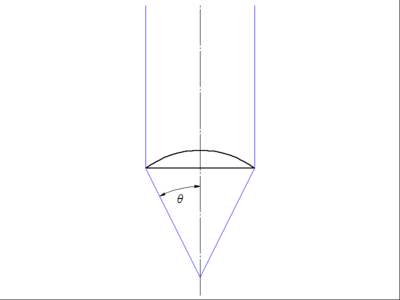
図：ピントがあった状態で光軸とレンズ最外周を透過する光線のなす角θの正弦が開口数。

　ここでnは対物レンズ前面と試料の間の媒体の屈折率で、乾燥系対物レンズなら空気の屈折率１、油浸対物レンズでは、油浸液の屈折率（約1.5)となる。sinθの最大値は１だから、乾燥系対物レンズのNAの最大値は１となる。一般に、高倍率の対物レンズほどNAは大きく、また、アクロマートとアポクロマートを比較すると、同倍率ならアポクロマートの方がNAが大きい。

NAと分解能

　クロス回折格子の観察像を用いて、(1)式の物理的背景を示す。クロス回折格子を用いているのは、後半での実験にクロス回折格子が必要であったためで、分解能の起源を理解するためだけなら、普通の回折格子で問題はない。

　今回用いたのは公称530本/mmのクロス回折格子なのだが、公称値から求めた回折角と実際の回折角が整合しなかったため、対物ミクロメータを用いて実測したところ、周期5.1ミクロン、本数にすると196本/mmであった(実は規格が5000本/インチである気がしてきた。)。さて、周期ｄの回折格子の1次の回折角は次式のm=1の場合で、dとして上記の値を用い、波長を550 nmとすると、回折角は6.2度で、その時の正弦は約0.11となる。

dsinθ=mλ　…………(3)

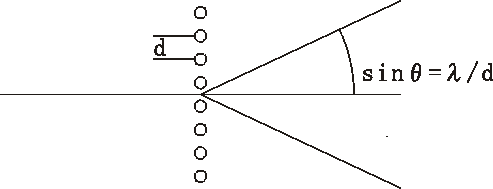
　アッベは顕微鏡で回折格子像が観察されるためには、対物レンズに直進する0次光に加えて、最低限1次の回折光が取り込まれる必要があることを見出した。言い換えれば、回折格子の1次の回折角の正弦値よりも大きなNA値の対物レンズでなければ、回折格子像は観察できないということである。

　下に、クロス回折格子像とその時の回折パターンの像を示す。回折パターンをどのように撮影したかを知りたい方は、回折格子を用いた分解能の議論の次にある「対物レンズ後ろ焦点面とベルトランレンズ」部分をご覧いただきたい。

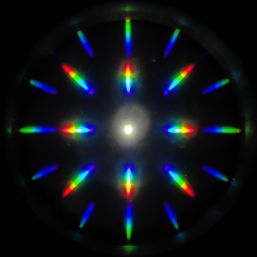
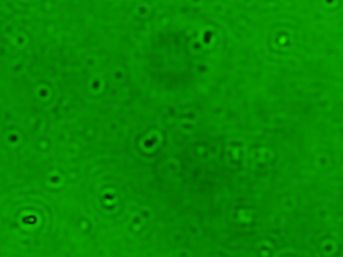
図：クロス回折格子像と対応する回折パターン

　右側の回折パターンの中心の白色部分が回折されずに直進した0次光である。左右と上下がそれぞれの周期構造による1次と2次の回折パターン。斜め45度やそれ以外の方向にも回折が生じている。図を見ると、1次の回折には青〜赤まで可視光全域が含まれているが、外周部分では回折光の赤色部分は取り込まれなくなっていたりする。このまま議論を進めてもよいのだけれど、波長を限定した方が、現象をすっきりと観察できそうなので、単色フィルターを使うことにした。

　波長が単色化されているので、細長く伸びていた回折スポットが丸い点状になっている。斜め方向の回折スポットがなくなっているが、これは、用いた波長では回折角が大きく、対物レンズに取り込まれなかったためである。ここから、対物レンズを通過する光を制限していく。

　回折パターンの水平と垂直方向の2次のスポットが入らなくなっているが、格子像はまだ問題なく見えているように思える。

　さらに入射光を制限して、0次と上下左右の1次の回折光のみが通過している。まだ、格子構造は見えている。

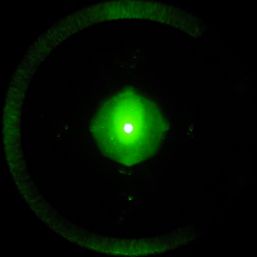
　残っていた上下左右の回折スポットも透過しないようにすると、格子構造が消えてしまう。この変化は劇的なものであるが、途中経過をよく見てみると、透過するスポット数の減少に伴って、格子構造のパターンに変化が生じていたことがわかる。

　図は左から2次の回折も含まれているもの、斜めの回折も残っているもの、上下左右の1次の回折のみのものである。2次の回折も含まれているものは、はっきりと正方形の格子が見えている。しかし、2次の回折光がなくなると、明るい部分の角が丸まって、きちんとした正方格子には見えなくなっている。そして、1次の回折だけのものは、穴あきの丸が集合したような構造に見えている。3つの写真でピントは同じに保っている。

　このシンプルな観察結果は、周期的な格子構造を観察するためには、0次光に加えて、少なくとも1次の回折光が対物レンズに取り込まれる必要があることを示している。縞構造の周期と回折角の式（(3)）より、開口数NAの対物レンズで観察できる最も細かい周期構造の間隔は

d=λ/NA …………(4)

であると結論できる。

格子間隔が同じでも波長が異なれば、回折角も変化する。

図に、450、500、550、600 nm光の回折パターンを示した。450nmや500nmでは見えていた回折パターンが550nmや600nmでは失われている。試みに、450nmと600nmのパターンを上下でつなぎ合わせてみた。黄色いサークルが対物レンズのNA相当である。

　単波長の光ほど回折角が小さいため、同じNAの対物レンズでも青色光なら回折光も取り込めるが、赤色光だと回折光を取り込めないといった事態も起こりうる。

図は白色光で、青色系の回折光のみ対物レンズに取り込めるように調整したものだが、この時点で、照明側のフィルターをいれて、青色光のみ、赤色光のみとしたのが次の写真である。

　当たり前の話であるが、青色光では周期構造が白色光よりコントラスト良くみえており、赤色光では見えなくなっている。ただし、見えている周期構造は決して正方格子ではなく、穴あき丸のつながりではある。

斜入射照明による分解能向上

　ここまでの議論を眺めながら、斜めから光を入射したらどうなるか気になった方もいるのではないかと思う。

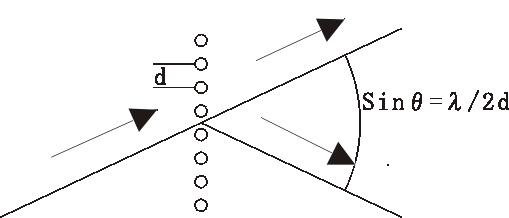
図：斜入射の場合の回折光。垂直入射に比べて、回折角が倍まで対物レンズに取り込まれる。

　図に示すように、対物レンズのNAギリギリの角度で照明光をいれると、垂直入射では取り込まれることのなかった1次の回折光が対物レンズの反対側の縁をとおって取り込まれるようになるはずだ。そこで、垂直入射では０次光しか透過しない状態にして、0次光が斜めから入射するように調整した。調整した結果の画像と対応する回折像を次に示す。観察対象は上と同じ、方眼のクロス回折格子である。

図：斜めからの照明にして、一方向に関しては1次の回折光（の片側）が入射するようにしたときの画像（左）

　見ての通り、1次の回折光が取り込まれている方向に関しては周期構造が観察されている。しかし、それと垂直の0次光しか取り込まれていない方向に関しては周期構造は再現できていない。このため、実物は方眼格子であるにも関わらず、縦縞の格子として観察されてしまっている。

 　0次光を斜入射にすると、上に示されているように、斜入射にした方向の分解能は垂直入射に対して、最大で2倍ほど向上する。この時の分解能の式は次のようになる。

d=λ/2NA …………(5)

斜入射照明による分解能向上は、偏斜照明と呼ばれる伝統的な技法で、1960年代ごろまでの研究用顕微鏡では普通に行える照明手法であったが、1970年代以降のシステム顕微鏡ではコンデンサが固定されてしまい、忘れられた照明手法となっている。

入射光の制限による像の変化

 　上に記したように、特定の方向の回折光のみで結像すると、もとの構造とは異なった像が形成される。上の例では、出現した周期は元の格子と同周期であったが、対物レンズ全面にスリットのあるマスクを付けて特定の回折光のみを選択すると、周期が異なる構造が出現する。取り付けたマスクと用いた対物レンズについては後ろの方の「用いた対物レンズ」の部分に記している。

　上段はマスクを付けていない画像で、クロス回折格子像が見えている。下段はマスクを装着して上下方向の回折スポットが入らないようにしたものである。斜入射の時と同じように1方向の回折スポットしか取り入れていないため、クロス回折格子ではなく、単純な縦縞になっている。縞の周期はクロス回折格子の周期と同じである。、

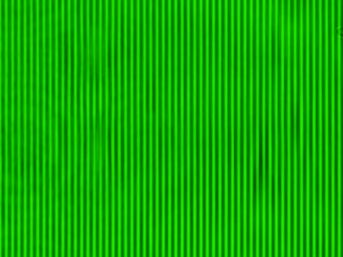
　続いては、クロス回折格子を45度回転したもの。マスクなしの画像を見ると、水平方向にはクロス回折格子の対角線方向に回折したスポットが広がっている。この対角線方向のスポットのみをスリットで選択したのが下の画像。最初の画像と同様に、縦縞となっているが、縞の周期はクロス回折格子の周期より短くなっている。元のクロス回折格子の方向とは異なっているけれども、45度回転した元画像から、どのような周期を読み取っているのかは理解できると思う。

最後は、約 30度回転させたもの。上の画像をみれば、どの回折スポットを拾ったのかは理解できる。回折角が大きいため、出現した縞の周期は45度回転よりも短くなっている。1次の回折光しか拾えていないこともあり、縞のコントラストは低下している。

対物レンズ後ろ焦点面とベルトランレンズ

　次の図は二重スリットを観察するときの光路を描いたものだ（スリットは紙面に⊥に伸びている）。図の上側は通常の観察で、スリットの一方から出た光と他方から出た光は像面で拡大像として結像している。二重スリットでは、干渉が生じ、二重スリットを通った光は、明暗のパターンを繰り返す。図では直進する光（0次光）と、最初に明るくなる方向（1次光）の光線を描いているけれども、それぞれの方向について、異なるスリットを通過した光は平行に対物レンズに入射するので、対物レンズの焦点位置（後ろ焦点面）で結像する。この面の像は明暗の縞模様の干渉像である。

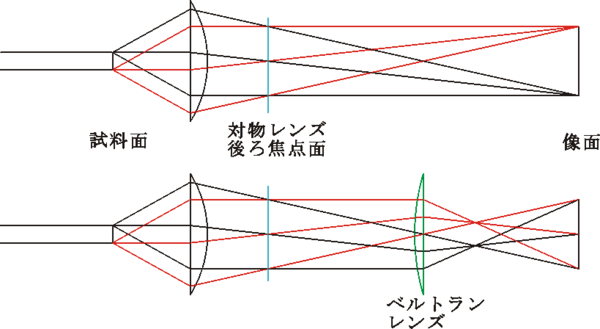
図：通常観察時の光路図とベルトランレンズをいれたときの光路図。像面に形成された画像を観察している。

　偏光顕微鏡には、「ベルトランレンズ」が装着されているものもあり、このレンズを光路に挿入すると、後ろ焦点面の像が、通常の像面に結像するようになる。干渉像が直接観察できるようになる。ベルトランレンズのない顕微鏡でも、接眼レンズを外して鏡筒をのぞき込めば、小さな後ろ焦点面の像が観察できるし、センタリングテレスコープ（位相差顕微鏡のリング調整に用いるアイピース）を用いると、大きな画像が観察できる。ベルトランレンズをいれて観察できる画像を、業界では「コノスコープ像」と呼んでいる。それに対して、通常の試料の拡大像は「オルソスコープ像」と呼ばれている。

実験に用いた対物レンズ

　回折光の取り込み角度範囲を変化させた実験ではNA可変の対物レンズを用いている。写真撮影用のレンズでは、絞り値を変えればNAが変化するけれども、普通の対物レンズには絞りがついていないので、NAを変えることはできない。しかし、顕微鏡対物レンズにも絞りが付いたものがある。

図：ニコンユニバーサルステージ用絞り付き対物レンズ

　写真はニコンのユニバーサルステージ用の対物レンズである。ユニバーサルステージは偏光顕微鏡のオプション器具で、試料の方向をかなりの範囲で自由に調整して観察できる器具である。ユニバーサルステージとの使用時に、ピントの合う範囲を広くするために、絞りが設けられた(NAが小さいとピントのあう範囲が広がる。)。

　後半の実験は、対物レンズの前に紙製のスリットを取り付けている。そのため、対物レンズ前面の径が大きく、スリットを取り付けやすい形状のものが適している。金属顕微鏡用の長作動対物レンズは全面が大きく、実験には適しているのだけれど、手持ちの有限光学系では、対物レンズ指定の鏡筒長を守ってのコノスコープ観察ができなかったので、オリンパスの生物用長作動対物レンズ(ULWDCDPlan20)を用いることにした。

図：オリンパス長作動対物レンズ（左）とスリット（右）

　オリンパスの対物レンズは対物レンズ単体では残存色収差があり、接眼レンズ系と合わせての収差補正なので、ニコンのシステムに装着すると色収差補正ができなくなるのだけれども、今回は単色光源を用いているので、色収差の心配はない。マスクは黒ケント紙の対物レンズの全面のサイズ(Φ25)に幅約0.5mmのスリットを切ったものを使っている。 

ヘルムホルツによる分解能の理論とレイリーによる比較

　アッベの議論は周期構造による回折を前提としている。これに対して、2点の識別に関する議論がヘルムホルツにより提唱された(顕微鏡分解能に関するAbbeとHelmholtzの理論の争点やその後の理論の発展については、中村日色, 顕微鏡の結像理論について, 応用物理　第21巻7号 251(13)、1952)を参考にした。J-Stageで自由にダウンロードできる。）。ヘルムホルツは自発光する2点の分解能について考察し、上記の5式と同じ

d=λ/2NA …………(5)(再掲)

を提唱したらしい。現在では自発光する2点に関する分解能はレイリーの分解能と言われることが多く、係数は(5)式とは異なった

d=λ/1.22NA あるいはd=0.61λ/NA…………(6)

が一般に流布している。

　アッベ理論とヘルムホルツ理論には2つの相違点がある。一つ目は観察対象で、アッベは回折格子を対象としたのに対し、ヘルムホルツは2つの点（もしくはスリット）を対象とした。もう一つは試料透過後の光の干渉性で、アッベは、それぞれのスリットを通過した光は互いに干渉するとしたが、ヘルムホルツは干渉しないとした。その後、レイリーが2点（2重スリット）の分解能について、非干渉と干渉の場合についての検討を行っている。ここでは、数式処理システムソフトの力を使って、レイリーの結果を再現して眺めてみようと思う。

　計算の概略は以下の通りである。

 　まずｘ座標上に原点を挟んでプラス方向とマイナス方向に、同じだけ離れた２つのディラックのデルタ関数を設定する。これが２本のスリットである。二重スリットに単色光を当てれば、干渉パターンが観察生じるが、これを数学的にはフーリエ変換という操作により再現できる。実際のスリットは有限幅なので、幅0のデルタ関数を用いた結果とはずれがあるのだけれども、実際の二重スリットの実験でも、スリット間隔に比べて、スリット幅は十分に細いため、デルタ関数を使った計算による結果と大きな違いは生じない。

　ちなみに、原点から±1/2のデルタ関数のフーリエ変換は

exp(ik/2)/sqrt(2π）とexp(-ik/2)/sqrt(2π）…………(7)

となる。スリットの位置の情報はexp(ik/2)の部分に含まれている。これら2つを加算してから2乗すれば、下に示した図の様な回折パターンの強度分布が得られる（それぞれを2乗してから和をとると、非干渉の強度パターンとなる。）。

　続いて、回折パターンを逆フーリエ変換する。とはいえ、単に逆フーリエ変換すると、もとのデルタ関数に戻ってしまう。これは、NAが無限大の対物レンズで結像した場合の結果に相当する。実際の対物レンズでは対物レンズのNAの範囲内にある回折光しか取り込めないので、数式上でも、その状況を再現する必要がある。そこで、回折の振幅パターンに原点付近のある幅だけ１でそれ以外は値が0に窓関数を掛け合わせた後に逆フーリエ変換する(実際には干渉パターンではなく、個々のスリットの干渉パターンを別々に逆フーリエ変換してから、最後に干渉させている。)。今回は窓の幅を2πとしている。窓の幅を2πとしたのは、こうすると、逆フーリエ変換した結果が

sin πx/πx…………(8)

と、原点で１、x=±１で0をよぎる関数となるためである(この結果は原点にスリットを置いた場合。スリットがx₀にあるなら、中心はずれ、そこが最大になる。）。レイリーによる分解能の定義は、二重スリットの一方の極大と、もう一方が0をよぎる位置が重なった時によるので、ピークと0を横切る点との差が1だと、間隔の調整が楽になる。

　まず、式（４）の照明光が垂直入射の場合の分解能のところから話を始めよう。この時、スリットは実空間座標で±0.82に設定している。

後ろ焦点面での干渉パターンと取り込み範囲を示す。

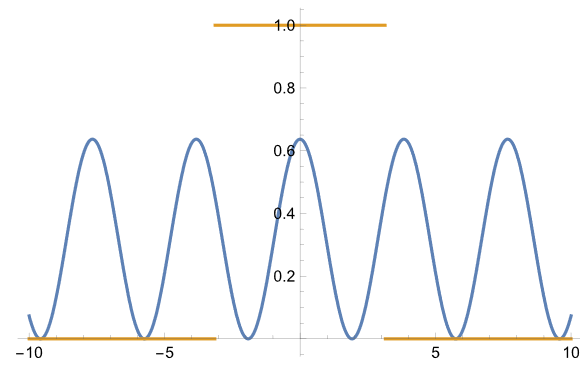
青が干渉強度パターンで、橙系が窓関数である。逆フーリエ変換は強度パターンの前の振幅を対象に行っている。

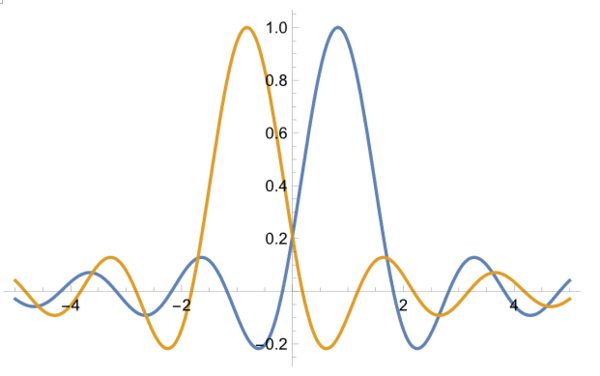
逆フーリエ変換をかけて得られた実空間での振幅パターン。この和をとって2乗すれば干渉パターンに。個別に2乗してから和をとれば非干渉パターンが得られる。

　まず干渉パターン。

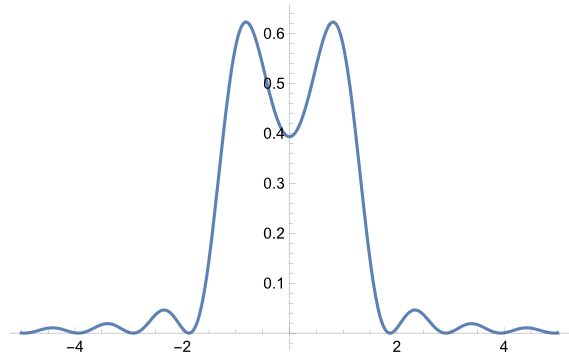
　続いて、非干渉パターン。

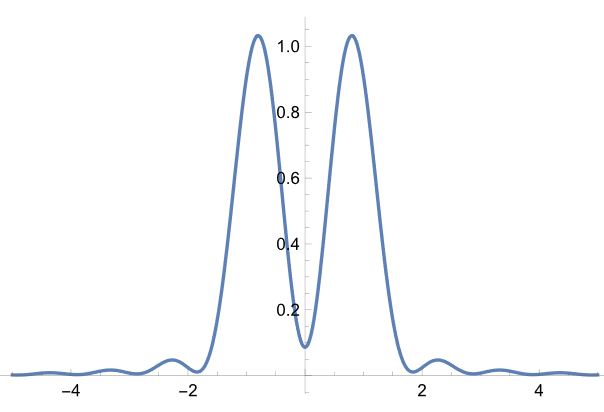
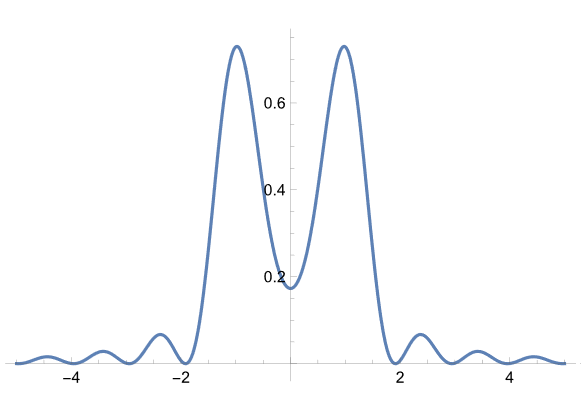
　非干渉の方が分離がはっきりしているが、干渉でも分離は確認できる。

　ところで、二重スリットの干渉では、回折格子による回折パターンとは異なり、回折光はピーク周りに広がりを持つ。回折格子の場合は、間隔が(4)式未満になった瞬間に1次の回折光は取り込めなくなるので、格子像は消失するけれども２本スリットなら、回折光の裾を拾えるので、間隔が(4)式未満になっても、瞬間にはスリット像が消失しないことが期待できる。試みに、（４）式の限界値の0.9倍の間隔でのパターンを計算してみると、

と、一応は分解して見えそうではある。

　続いて、式(6)のレイリーの分解能までスリットが近づいた場合。

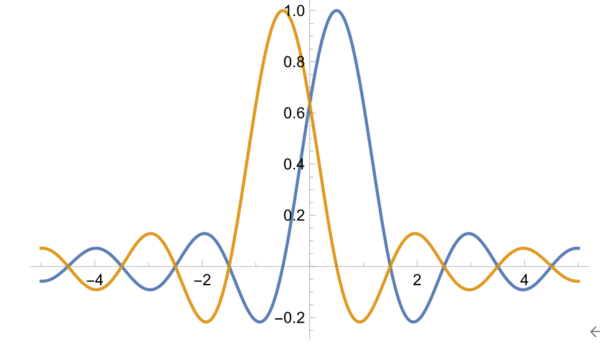
図：実空間で±1/2にあるスリットからの回折パターン。図は振幅で光強度は振幅の2乗となる。一方のピークは、もう一方が0となる地点になっている。

　非干渉性の場合は、それぞれの回折光を2乗して強度としてから加算すればよい。まず両者を2乗してみる。

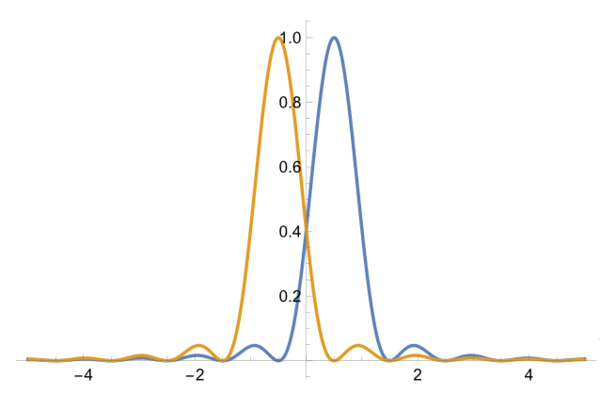
そして、その和は

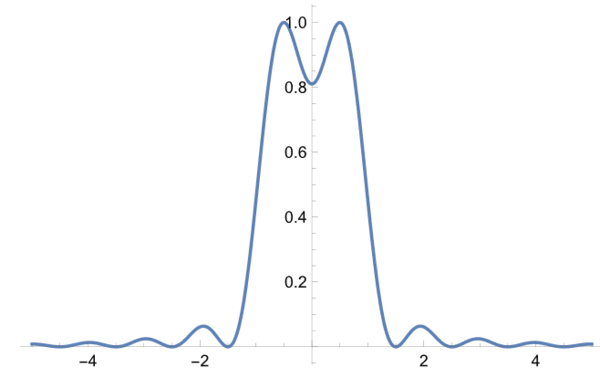
となり、2本の線としての識別が可能であるとされている。一方、干渉性の場合には、振幅レベルで和を取る必要があり、和を求めてみると

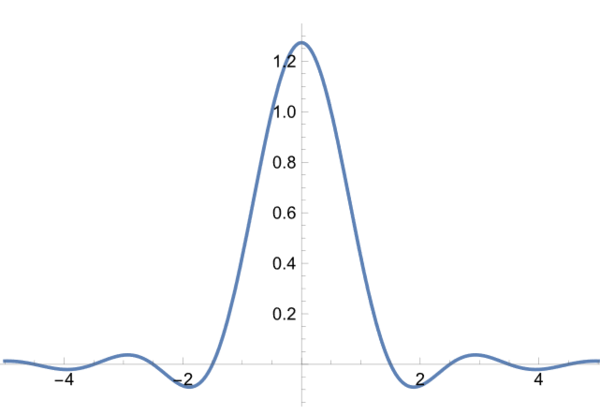
1本のピークとなってしまい、光強度も

当然ながら1本ピークとなってしまい、分離できていない。

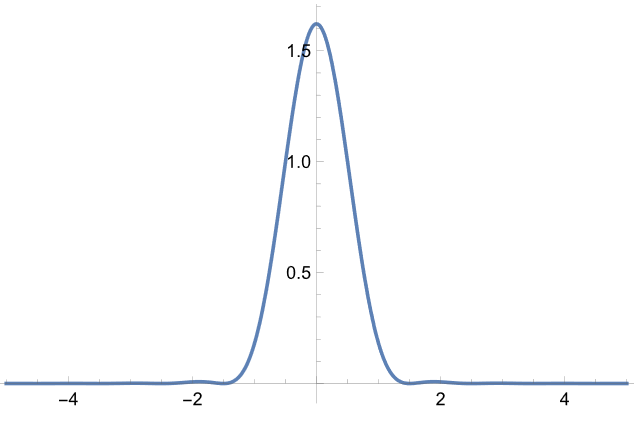
　続いて、（５）式の係数が２の場合を検討する。まず非干渉の場合を示すと

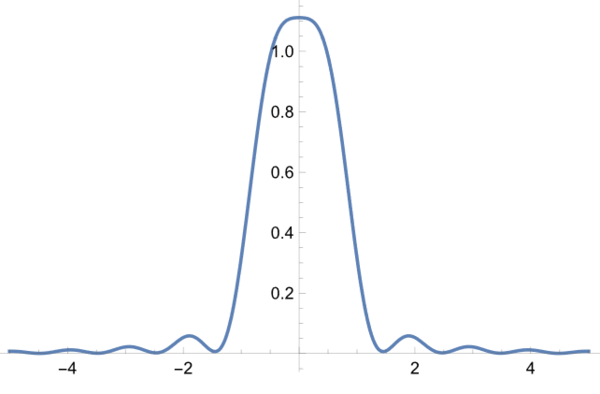
と幅のある1本の構造となっており、分解できたとはいいがたい印象である（それゆえ、ヘルムホルツが出した（５）式の根拠が不思議になっている。）。一方、干渉条件では

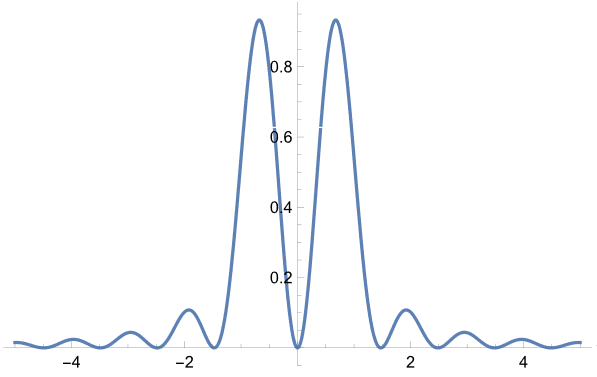
はっきりと2本に分離できている。より幅のあるレイリー条件で分離できていなかったのに、それ以下で分解できるようになるのは、先ほどは2本スリットで光が同位相で通過していたのに対して、斜入射ではスリット通過時の光の位相に差があり、対物のNAギリギリの入射光の回折条件では2つのスリット通過時には逆位相となっているためである。

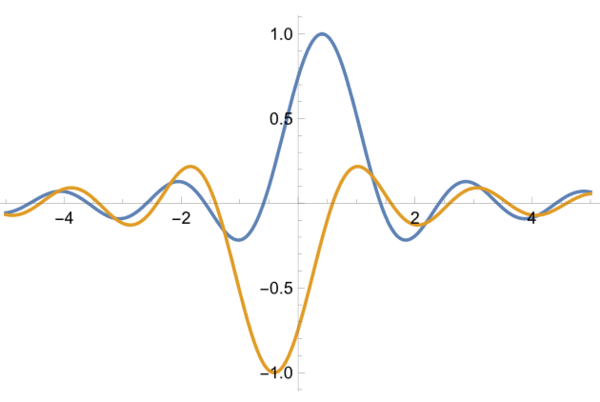
図は2本スリットが逆位相の場合の回折パターンであるが、原点では両方のスリットからの振幅が逆位相で完全に打ち消しあう配置となっている。このため、きっちりと2本に分離したピークが出現した。ただし、像の間隔は元の幅の1.7倍程度になってしまっている。2重スリットであることはわかっても、スリット間隔は正しく再現されてはいないのである。

　2つのスリットでの位相が逆なら、スリット間隔によらず、スリット像の真ん中の光強度は0となり、2本線は分離されるはずである。このアイデアは、光リソグラフィーでは活用されているらしいのだけれど、顕微鏡の場合は、位相差のもとが斜入射による光路差で、それは2点間の距離にも依存するので、最大NAで入射した光でも、分解能以下の距離では位相差はπには満たなくなってしまう。とはいえ、垂直入射で(4)式以下でも分解できているので、検討してみる価値はある気がする。試みに、λ/(2.5NA)で計算してみると

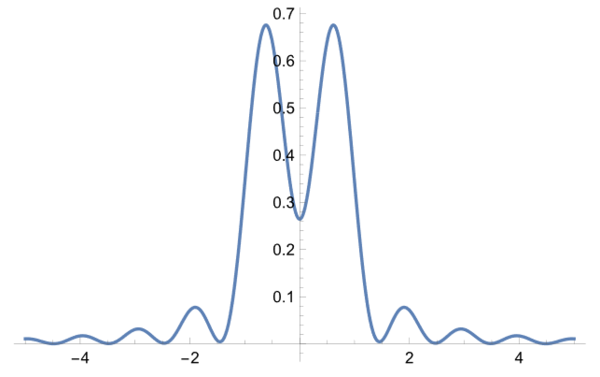
2本線は一応分離はしているけれども、ピーク間隔は1.9倍程度の値となってしまっている。(5)式条件の場合と異なり、原点でも回折強度が0にはなっていないが、これは、2つのスリット間の位相がπよりも小さくなっているためである。

コヒーレント照明とインコヒーレント照明

　アッベとヘルムホルツの理論に関しては、照明光の干渉性により、どちらの議論が適用されるべきかが変わってしまうので、実際の顕微鏡照明が干渉性(コヒーレント）であるか、非干渉性（インコヒーレント）であるかが問題となった。

　顕微鏡の本を眺めると、コンデンサレンズを絞って低ＮＡにするとコヒーレント、広げてＮＡを高くするとインコヒーレントになるとの説明をよく見かける。

　この説明が正しいかを考えるため、少し寄り道になるけれども、ヤングの二重スリットの実験を通して、干渉性と非干渉性について検討しておこう。ヤングの実験は二重スリットによる干渉により光の波動性を示したもので、次の図の上のように、二重スリットの前に単スリットを置いた配置で行われる。

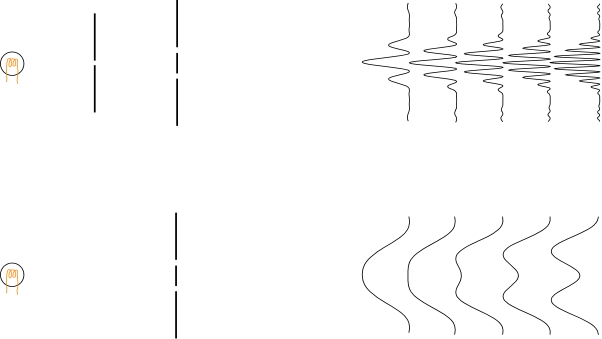
　単スリットがある場合には二重スリットによる干渉構造が観察され、スリット間隔が広がるほど干渉パターンは狭くなる。もし、単スリットがないと、図の下のように二重スリットによる干渉構造は発生せず、二重スリットのそれぞれによる回折強度が加算された構造となる。

　単スリットがない場合に干渉パターンが観察されないのは、光源の異なる部分からの光が相互に干渉しないためであるとの説明が行われることが多い。これは、顕微鏡においてNAを大きくした場合のインコヒーレント照明の説明と同じである。これに対して、勝田仁之氏は「再考：ヤングの二重スリット実験」（中央大学付属中学校・高等学校　紀要（教育・研究）第31号(2017)、または　物理教育通信　170号、P13 (2017)）において、単スリットの役割は二重スリットに到達する光の位相をそろえることであることを論証している。勝田氏の論証とは異なるが、光子が自分自身と干渉することを考えると、単スリットがなくても、光源からの光はスリット通過後に自分自身とは干渉して、スクリーンのある場所の光点となる。光源の別の場所から来た光子も自身の干渉規則に従った光点となる。しかし、光子の到来する方向により、スリットにおける位相差はことなり、その結果として、干渉パターンの極大、極小位置にもずれが生じる。光子の到来方向に幅があると、異なる極大。極小位置の干渉が平均化されてしまい、見かけ上は干渉が生じなくなる。しかし、うらでは光子は干渉はしている。

　勝田氏と同様の立場からは、顕微鏡の照明でも事情は同じで、コンデンサのNAを開いた場合でも、個々の光子は干渉しているが、光の入射方向と、微細構造の間隔の関係により、位相差が0のものからπを超えるものまで連続して分布しており、得られる像は、それらの平均的な合算によるものとなってしまう。見かけはインコヒーレントだとしても、プロセスはコヒーレント結像の和として考える方が納得できる。